Loi du χ² non centrée

Loi du χ2 non centré
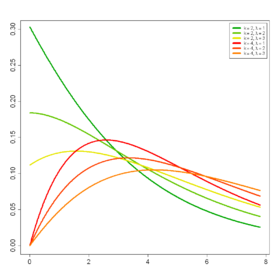Densité de probabilité
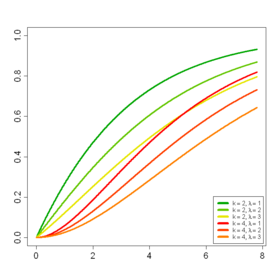Fonction de répartition
Paramètres	${\displaystyle k>0\,}$ (degrés de liberté) ${\displaystyle \lambda >0\,}$ paramètre de décentralisation
Support	${\displaystyle x\in [0;+\infty [\,}$
Densité de probabilité	${\displaystyle {\frac {1}{2}}{\rm {e}}^{-(x+\lambda )/2}\left({\frac {x}{\lambda }}\right)^{k/4-1/2}I_{k/2-1}({\sqrt {\lambda x}})}$
Fonction de répartition	${\displaystyle 1-Q_{\frac {k}{2}}\left({\sqrt {\lambda }},{\sqrt {x}}\right)}$ avec la fonction Q de Marcum ${\displaystyle Q_{M}(a,b)}$
Espérance	${\displaystyle k+\lambda \,}$
Variance	${\displaystyle 2(k+2\lambda )\,}$
Asymétrie	${\displaystyle {\frac {2^{3/2}(k+3\lambda )}{(k+2\lambda )^{3/2}}}}$
Kurtosis normalisé	${\displaystyle {\frac {12(k+4\lambda )}{(k+2\lambda )^{2}}}}$
Fonction génératrice des moments	${\displaystyle {\frac {\exp \left({\frac {\lambda t}{1-2t}}\right)}{(1-2t)^{k/2}}}}$ pour t < 1/2
Fonction caractéristique	${\displaystyle {\frac {\exp \left({\frac {i\lambda t}{1-2it}}\right)}{(1-2it)^{k/2}}}}$
modifier

En théorie des probabilités et en statistique, la loi du χ² non centrée est une loi de probabilité qui généralise la loi du χ². Cette loi apparait lors de tests statistiques, par exemple pour le maximum de vraisemblance.

Motivations

Soit X_i, k variables aléatoires indépendantes de loi normale de moyennes ${\displaystyle \mu _{i}}$ et variances ${\displaystyle \sigma _{i}^{2}}$. Alors la variable aléatoire

${\displaystyle \sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}}$

suit une loi du χ² non centrée. Elle dépend de deux paramètres : k qui spécifie le nombre de degrés de liberté (c'est-à-dire le nombre de X_i), et λ qui est en lien avec la moyenne des variables X_i par la formule :

${\displaystyle \lambda =\sum _{i=1}^{k}\left({\frac {\mu _{i}}{\sigma _{i}}}\right)^{2}.}$

${\displaystyle \lambda }$ est parfois appelé le paramètre de décentralisation. Certaines références définissent λ différemment, comme la moyenne de la somme ci-dessus ou comme sa racine carrée.

Cette loi apparait en statistique multivariée, elle est issue de la loi normale multidimensionnelle. Comme la loi du χ² est le carré de la norme du vecteur aléatoire défini à partir des variables de loi ${\displaystyle {\mathcal {N}}(0_{k},I_{k})}$ (c'est-à-dire le carré de la distance entre l'origine et un point donné par cette loi), la loi du χ² non centrée est le carré de la norme d'un vecteur aléatoire de loi ${\displaystyle {\mathcal {N}}(\mu ,I_{k})}$. Ici 0_k est le vecteur nul de longueur k, ${\displaystyle \mu =(\mu _{1},...,\mu _{k})}$ et I_k est la matrice unité de taille k.

Définition

La densité de probabilité est donnée par :

${\displaystyle {\begin{cases}f_{X}(x;k,\lambda )=\sum _{i=0}^{\infty }{\dfrac {{\rm {e}}^{-\lambda /2}(\lambda /2)^{i}}{i!}}f_{Y_{k+2i}}(x)&{\text{ si }}x>0\\0&{\text{ sinon}}\end{cases}}}$

où Y_q est de loi du χ² à q degrés de liberté.

De cette représentation, la loi du χ² non centrée est vue comme une loi mélange de loi du ${\displaystyle \chi ^{2}}$. Supposons que la variable J suit une loi de Poisson avec moyenne λ/2, et que la loi conditionnelle de Z sachant J = i est la loi du χ² à k+2i degrés de liberté. Alors la loi (non conditionnelle) de Z est la loi du χ² non centrée à k degrés de liberté, et avec paramètre de décentralisation ${\displaystyle \lambda }$.

D'une autre part, la densité peut être écrite sous la forme

${\displaystyle f_{X}(x;k,\lambda )={\frac {1}{2}}{\rm {e}}^{-(x+\lambda )/2}\left({\frac {x}{\lambda }}\right)^{k/4-1/2}I_{k/2-1}({\sqrt {\lambda x}})}$

où I_ν(z) est la fonction de Bessel modifiée du premier type donnée par

${\displaystyle I_{a}(y)=(y/2)^{a}\sum _{j=0}^{\infty }{\frac {(y^{2}/4)^{j}}{j!\Gamma (a+j+1)}}.}$

En utilisant la relation entre les fonctions de Bessel et hypergéométrique, la densité peut également être écrite sous la forme^[1] :

${\displaystyle f_{X}(x;k,\lambda )={{\rm {e}}^{-\lambda /2}}_{0}F_{1}(;k/2;\lambda x/4){\frac {1}{2^{k/2}\Gamma (k/2)}}{\rm {e}}^{-x/2}x^{k/2-1}.}$

Siegel (1979) considère plus particulièrement le cas k=0 (0 degré de liberté), dans ce cas la loi est atomique en 0.

Propriétés

Fonction génératrice des moments

La fonction génératrice des moments est donnée par

${\displaystyle M(t;k,\lambda )={\frac {\exp \left({\frac {\lambda t}{1-2t}}\right)}{(1-2t)^{k/2}}}.}$

Moments

Les premiers moments sont :

${\displaystyle \mu _{1}^{'}=k+\lambda }$

${\displaystyle \mu _{2}^{'}=(k+\lambda )^{2}+2(k+2\lambda )}$

${\displaystyle \mu _{3}^{'}=(k+\lambda )^{3}+6(k+\lambda )(k+2\lambda )+8(k+3\lambda )}$

${\displaystyle \mu _{4}^{'}=(k+\lambda )^{4}+12(k+\lambda )^{2}(k+2\lambda )+4(11k^{2}+44k\lambda +36\lambda ^{2})+48(k+4\lambda )}$

Les premiers moments centrés sont :

${\displaystyle \mu _{2}=2(k+2\lambda )\,}$

${\displaystyle \mu _{3}=8(k+3\lambda )\,}$

${\displaystyle \mu _{4}=12(k+2\lambda )^{2}+48(k+4\lambda )\,}$

Le n-ième cumulant est

${\displaystyle K_{n}=2^{n-1}(n-1)!(k+n\lambda ).\,}$

Ainsi

${\displaystyle \mu _{n}^{'}=2^{n-1}(n-1)!(k+n\lambda )+\sum _{j=1}^{n-1}{\frac {(n-1)!2^{j-1}}{(n-j)!}}(k+j\lambda )\mu _{n-j}^{'}.}$

Fonction de répartition

En utilisant encore la relation entre les lois du χ² centrée et non centrée, la fonction de répartition peut s'écrire sous la forme

${\displaystyle P(x;k,\lambda )={\rm {e}}^{-\lambda /2}\;\sum _{j=0}^{\infty }{\frac {(\lambda /2)^{j}}{j!}}Q(x;k+2j)}$

où Q(x ; k) est la fonction de répartition de la loi du χ² à k degrés de liberté donnée par :

${\displaystyle Q(x;k)={\frac {\gamma (k/2,x/2)}{\Gamma (k/2)}}\,}$

et où γ(k,z) est la fonction gamma incomplète.

La fonction Q de Marcum Q_M(a,b) peut également être utilisée pour formuler la fonction de répartition^[2] :

${\displaystyle P(x;k,\lambda )=1-Q_{\frac {k}{2}}\left({\sqrt {\lambda }},{\sqrt {x}}\right)}$

Approximation

Sankaran^[3] propose plusieurs formes approchées de la fonction de répartition. Dans un article précédent^[4], il formule l'expression suivante :

${\displaystyle P(x;k,\lambda )\approx \Phi \left[{\frac {({\frac {x}{k+\lambda }})^{h}-(1+hp(h-1-0.5(2-h)mp))}{h{\sqrt {2p}}(1+0.5mp)}}\right]}$

où

${\displaystyle \Phi (\cdot )\,}$ est la fonction de répartition de la loi normale,

${\displaystyle h=1-{\frac {2}{3}}{\frac {(k+\lambda )(k+3\lambda )}{(k+2\lambda )^{2}}}\,,}$

${\displaystyle p={\frac {k+2\lambda }{(k+\lambda )^{2}}},}$

${\displaystyle m=(h-1)(1-3h)\,.}$

Cette approximation ainsi que d'autres sont données dans un livre ultérieur^[5].

Pour approcher la loi du χ², le paramètre de décentralisation λ est égal à zéro.

Liens avec d'autres lois

• Si V est de loi du χ², ${\displaystyle V\sim \chi _{k}^{2}}$, alors ${\displaystyle V}$ est également de loi du χ² non centrée : ${\displaystyle V\sim {\chi '}_{k}^{2}(0)}$.
• Si ${\displaystyle V_{1}\sim {\chi '}_{k_{1}}^{2}(\lambda )}$, ${\displaystyle V_{2}\sim {\chi '}_{k_{2}}^{2}(0)}$, et V₁ et V₂ sont indépendantes, alors ${\displaystyle {\frac {V_{1}/k_{1}}{V_{2}/k_{2}}}}$ est de loi de Fisher non centrée : ${\displaystyle {\frac {V_{1}/k_{1}}{V_{2}/k_{2}}}\sim F'_{k_{1},k_{2}}(\lambda )}$.
• Si ${\displaystyle J\sim {\mathcal {P}}({\frac {\lambda }{2}})}$, où ${\displaystyle {\mathcal {P}}}$ désigne la loi de Poisson, alors ${\displaystyle \chi _{k+2J}^{2}\sim {\chi '}_{k}^{2}(\lambda )}$
• Approximation par la loi normale^[6] : si ${\displaystyle V\sim {\chi '}_{k}^{2}(\lambda )}$, alors ${\displaystyle {\frac {V-(k+\lambda )}{\sqrt {2(k+2\lambda )}}}\to {\mathcal {N}}(0,1)}$ en probabilité lorsque ${\displaystyle k\to \infty }$ ou ${\displaystyle \lambda \to \infty }$.

Transformations

Sankaran (1963) étudie les transformations de la forme ${\displaystyle z=[(X-b)/(k+\lambda )]^{1/2}}$. Il analyse le développement des cumulants de z de l'ordre de ${\displaystyle O((k+\lambda )^{-4})}$ et montre que les choix suivants de b donnent les résultats raisonnables suivants :

• ${\displaystyle b=(k-1)/2}$ rend le second cumulant de z approximativement indépendant de λ,
• ${\displaystyle b=(k-1)/3}$ rend le troisième cumulant de z approximativement indépendant de λ,
• ${\displaystyle b=(k-1)/4}$ rend le quatrième cumulant de z approximativement indépendant de λ.

De plus, une transformation plus simple, ${\displaystyle z_{1}=(X-(k-1)/2)^{1/2}}$, peut être utilisée comme fonction de stabilisation de variance qui produit une variable aléatoire de moyenne ${\displaystyle (\lambda +(k-1)/2)^{1/2}}$ et de variance ${\displaystyle O((k+\lambda )^{-2})}$.

L'utilisation de ces transformations peut être altérée par le fait de considérer les racines carrées de nombres négatifs.

Différentes lois du χ et χ²

Lois	en fonction de variables de loi normale
loi du χ²	${\displaystyle \sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}}$
loi du χ² non centrée	${\displaystyle \sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}}$
loi du χ	${\displaystyle {\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}}}}$
loi du χ non centrée	${\displaystyle {\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}}}}$

Références

• Abramowitz, M. and Stegun, I.A. (1972), Handbook of Mathematical Functions, Dover. Section 26.4.25.
• Johnson, N. L., Kotz, S., Balakrishnan, N. (1970), Continuous Univariate Distributions, Volume 2, Wiley. (ISBN 0-471-58494-0)
• Muirhead, R. (2005) Aspects of Multivariate Statistical Theory (2nd Edition). Wiley. (ISBN 0471769851)
• Siegel, A.F. (1979), "The noncentral chi-squared distribution with zero degrees of freedom and testing for uniformity", Biometrika, 66, 381–386

• Portail des probabilités et de la statistique