Loi de Student

Loi t de Student
Densité de probabilité
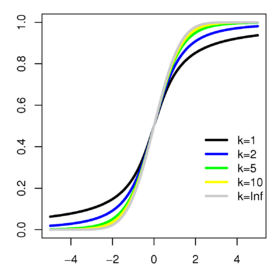Fonction de répartition
Paramètres	k > 0 (degrés de liberté)
Support	${\displaystyle x\in \mathbb {R} }$
Densité de probabilité	${\displaystyle f_{T}(t)={\frac {1}{\sqrt {k\pi }}}{\frac {\Gamma ({\frac {k+1}{2}})}{\Gamma ({\frac {k}{2}})}}\left(1+{\frac {t^{2}}{k}}\right)^{-{\frac {k+1}{2}}}}$
Fonction de répartition	${\displaystyle {\begin{matrix}{\frac {1}{2}}+x\Gamma \left({\frac {k+1}{2}}\right){\frac {\,_{2}F_{1}\left({\frac {1}{2}},{\frac {k+1}{2}};{\frac {3}{2}};-{\frac {x^{2}}{k}}\right)}{{\sqrt {k\pi }}\,\Gamma \left({\frac {k}{2}}\right)}}\end{matrix}}}$ où 2F1 est la fonction hypergéométrique
Espérance	si k ≤ 1 : forme indéterminée si k > 1 : 0
Médiane	0
Mode	0
Variance	si k ≤ 1 : forme indéterminée si 1 < k ≤ 2 : +∞ si k > 2 : ${\displaystyle {\frac {k}{k-2}}}$
Asymétrie	si k ≤ 3 : forme indéterminée si k > 3 : 0
Kurtosis normalisé	si k ≤ 2 : forme indéterminée si 2 < k ≤ 4 : +∞ si k > 4 : ${\displaystyle {\frac {6}{k-4}}}$
modifier

En théorie des probabilités et en statistique, la loi de Student est une loi de probabilité, faisant intervenir le quotient entre une variable suivant une loi normale centrée réduite et la racine carrée d'une variable distribuée suivant la loi du χ².

Elle est notamment utilisée pour les tests de Student, la construction d'intervalle de confiance et en inférence bayésienne.

Définition

Soit Z une variable aléatoire de loi normale centrée et réduite et soit U une variable indépendante de Z et distribuée suivant la loi du χ² à k degrés de liberté. Par définition, la variable

${\displaystyle T={\frac {Z}{\sqrt {U/k}}}}$

suit une loi de Student à k degrés de liberté.

${\displaystyle U=\sum _{i=1}^{k}X_{i}^{2}}$, alors ${\displaystyle U\sim \chi _{k}^{2}}$, où les X_i sont k variables aléatoires réelles i.i.d. de loi normale centrée-réduite.

Propriétés

Densité

La densité de T, notée f_T, est donnée par :

${\displaystyle f_{T}(t)={\frac {1}{\sqrt {k\pi }}}{\frac {\Gamma ({\frac {k+1}{2}})}{\Gamma ({\frac {k}{2}})}}\left(1+{\frac {t^{2}}{k}}\right)^{-{\frac {k+1}{2}}},\;{\textrm {pour}}\;k>0}$.

où Γ est la fonction Gamma d'Euler.

La densité f_T associée à la variable T est symétrique, centrée en 0 et en forme de cloche.

Espérance

Son espérance ne peut pas être définie pour k = 1, et est nulle pour k > 1.

Variance

Sa variance est infinie pour k = 2 et vaut k/k – 2 pour k > 2.

Comportement limite

Lorsque k est grand, la loi de Student converge vers la loi normale centrée réduite. Une manière simple de le démontrer est d'utiliser le lemme de Scheffé.

Histoire

Le calcul de la loi de Student a été décrit en 1908 par William Gosset^[1] alors qu'il était employé à la brasserie Guinness à Dublin. Son patron, sans doute pour des raisons liées à la concurrence, interdisait à ses employés de publier sous leur propre nom. Pour cette raison Gosset choisit un pseudonyme, Student, qui, en anglais, signifie étudiant. Le test t et la théorie sont devenus célèbres par les travaux de Ronald Fisher qui a donné à la loi le nom de « loi de Student »^[2],[3].

La loi de Student dans l'échantillonnage

Soient X₁, ..., X_n, n variables aléatoires mutuellement indépendantes et distribuées suivant une même loi normale ${\displaystyle {\mathcal {N}}(\mu ,\sigma ^{2})}$ d’espérance μ et de variance σ² qui correspondent à un échantillon de taille n. Considérons la moyenne empirique

${\displaystyle {\overline {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}}$

et l'estimateur sans biais de la variance

${\displaystyle S^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}(X_{i}-{\overline {X}})^{2}}$.

Par normalisation, la variable aléatoire

${\displaystyle Z={\frac {{\overline {X}}-\mu }{\sigma /{\sqrt {n}}}}}$

suit une loi normale standard (d’espérance 0 et de variance 1). La variable aléatoire obtenue en remplaçant σ par S dans ${\displaystyle Z}$ est

${\displaystyle T={\frac {{\overline {X}}-\mu }{S/{\sqrt {n}}}}}$,

${\displaystyle T}$ suit la loi de Student à n – 1 degrés de liberté. Ce résultat est utile pour trouver des intervalles de confiance quand σ² est inconnue, comme indiqué plus bas.

Pour justifier cela, on introduit la variable aléatoire

${\displaystyle U={\frac {1}{\sigma ^{2}}}\sum _{i=1}^{n}(X_{i}-{\overline {X}})^{2}}$

qui permet d'écrire ${\displaystyle {\frac {S^{2}}{\sigma ^{2}}}={\frac {U}{n-1}}}$ et

${\displaystyle T={\frac {{\overline {X}}-\mu }{\sigma /{\sqrt {n}}}}{\frac {1}{S/\sigma }}={\frac {Z}{\sqrt {U/(n-1)}}}}$

Pour terminer il faut montrer que Z et U sont indépendantes et que U suit une loi du χ² à n – 1 degrés de liberté. C'est précisément ce que montre le Théorème de Cochran.

Remarquons la perte d'un degré de liberté car même s'il y a n variables aléatoires X_i indépendantes, les ${\displaystyle X_{i}-{\overline {X}}}$ ne le sont pas puisque leur somme fait 0.

Application : intervalle de confiance associé à l’espérance d’une variable de loi normale de variance inconnue

Ce chapitre présente une méthode pour déterminer l'intervalle de confiance de l’espérance μ d’une loi normale. Notons que si la variance est connue, il vaut mieux utiliser directement la loi normale avec la moyenne ${\displaystyle {\overline {X}}}$.

avec ${\displaystyle {\overline {X}}}$, l'estimateur ponctuel de l'espérance et ${\displaystyle S}$, l'estimateur non biaisé de l'écart-type définis ci-dessus.

${\displaystyle t_{\gamma }^{k}}$ est le quantile d’ordre ${\displaystyle 1-\gamma }$ de la loi de Student à k degrés de liberté, c'est l'unique nombre qui vérifie

${\displaystyle \mathbb {P} (T\leq t_{\gamma }^{k})=1-\gamma }$

lorsque T suit la loi de Student à k degrés de liberté.

Par exemple, voici les tailles mesurées en cm sur un échantillon de 8 personnes

i	1	2	3	4	5	6	7	8
${\displaystyle x_{i}}$	155	160	161	167	171	177	180	181

on en calcule la moyenne statistique ${\displaystyle {\overline {x}}}$ et la variance sans biais ${\displaystyle s^{2}}$ :

${\displaystyle {\overline {x}}={\frac {1}{8}}\sum _{i=1}^{8}x_{i}=169}$

${\displaystyle s^{2}={\frac {1}{7}}\sum _{i=1}^{8}(x_{i}-{\overline {x}})^{2}=96{,}{\underline {857142}}}$

Prenons un risque ${\displaystyle \alpha =10\%}$, donc un niveau de confiance ${\displaystyle 1-\alpha =90\%}$. Aux arrondis près, le tableau des quantiles ci-dessous donne ${\displaystyle t_{5\%}^{7}=1{,}895}$, et l'intervalle de confiance est

${\displaystyle \left[{\overline {x}}-t_{5\%}^{7}{\frac {s}{\sqrt {8}}};{\overline {x}}+t_{5\%}^{7}{\frac {s}{\sqrt {8}}}\right]=\left[162{,}4;175{,}6\right].}$

La probabilité que la taille moyenne de la population soit dans cet intervalle est de 90 %. Or la taille moyenne des français est de 177 cm, mais 177 n'appartient pas à cet intervalle de confiance, on peut alors dire que cet échantillon ne correspond pas à la population française, avec 10 % d'erreur. C'est un exemple d'application du test de Student.

Le graphique suivant illustre la notion de niveau de confiance en tant qu'intégrale de la fonction ${\displaystyle f_{T}}$ pour ${\displaystyle k=7}$, représentée par l'aire de la zone en bleu.

En résumé, pour un échantillon ${\displaystyle x_{1},x_{2},...x_{n}}$ d’une loi normale d'espérance μ, l’intervalle de confiance de μ au niveau ${\displaystyle 1-\alpha }$ est :

${\displaystyle \left[\,{\overline {x}}-t_{\alpha /2}^{n-1}{\frac {s}{\sqrt {n}}},{\overline {x}}+t_{\alpha /2}^{n-1}{\frac {s}{\sqrt {n}}}\,\right]}$,

avec

${\displaystyle {\overline {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}}$,

${\displaystyle s^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}$,

et ${\displaystyle t_{\gamma }^{k}}$ le quantile d’ordre ${\displaystyle 1-\gamma }$ de la loi de Student à k degrés de liberté.

Lois apparentées

• ${\displaystyle X\sim \mathrm {t} (k=1)~}$ suit une loi de Cauchy : ${\displaystyle X\sim \operatorname {Cauchy} (0,1)}$.
• ${\displaystyle \mathrm {t} (k)\,{\xrightarrow {\mathcal {L}}}\,{\mathcal {N}}(0,1)}$ : la loi de Student converge en loi vers la loi normale.
• Si ${\displaystyle X\sim \mathrm {t} (k)\!}$ suit une loi de Student alors X² suit une loi de Fisher : ${\displaystyle X^{2}\sim \operatorname {F} (\nu _{1}=1,\nu _{2}=k)}$
• ${\displaystyle X\sim \mathrm {t} (k)~}$ a une loi de Student si ${\displaystyle \sigma ^{2}\sim {\mbox{Inv-}}\chi ^{2}(k,1)\!}$ suit une loi inverse-χ² et ${\displaystyle X\sim {\mathcal {N}}(0,\sigma ^{2})\!}$ suit une loi normale.

Tableau des valeurs du quantile

Le tableau suivant fournit les valeurs de certains quantiles de la loi de Student pour différents degrés de liberté k. Pour chaque valeur de ${\displaystyle 1-\alpha }$, le quantile donné est tel que la probabilité pour qu'une variable suivant une loi de Student à k degrés de liberté lui soit inférieur est de ${\displaystyle 1-\alpha }$. Ainsi, pour ${\displaystyle 1-\alpha =0{,}95}$ et k = 7, si T suit une loi de Student à 7 degrés de liberté, on lit dans la table que ${\displaystyle \mathbb {P} (T\leq 1{,}895)=0{,}95}$. Pour un intervalle de pari bilatéral à 95 %, on prendra le quantile à 97,5 % : ${\displaystyle \mathbb {P} (T\in [-2{,}365;2{,}365])=0{,}95}$.

Notons également que si l'on note ${\displaystyle t_{\alpha }^{k}}$ le quantile d'ordre ${\displaystyle 1-\alpha }$ de la loi de Student à k degrés de liberté alors on a ${\displaystyle t_{\alpha }^{k}=-t_{1-\alpha }^{k}}$. Avec l'exemple précédent, on a ${\displaystyle \mathbb {P} (T\leq 1{,}895)=0{,}95}$ et ${\displaystyle \mathbb {P} (T\leq -1{,}895)=0{,}05}$

Un tableur standard permet de calculer ces quantiles de manière plus précise,

par exemple LOI.STUDENT.INVERSE(0,95;7) donne ${\displaystyle 1{,}89457860509001}$

.

On obtient la même valeur avec la commande qt(0.95,7) du logiciel R. En général qt(${\displaystyle 1-\alpha }$,${\displaystyle k}$) donne ${\displaystyle t_{\alpha }^{k}}$.

1–α	75 %	80 %	85 %	90 %	95 %	97,5 %	99 %	99,5 %	99,75 %	99,9 %	99,95 %
k
1	1,000	1,376	1,963	3,078	6,314	12,71	31,82	63,66	127,3	318,3	636,6
2	0,816	1,061	1,386	1,886	2,920	4,303	6,965	9,925	14,09	22,33	31,60
3	0,765	0,978	1,250	1,638	2,353	3,182	4,541	5,841	7,453	10,21	12,92
4	0,741	0,941	1,190	1,533	2,132	2,776	3,747	4,604	5,598	7,173	8,610
5	0,727	0,920	1,156	1,476	2,015	2,571	3,365	4,032	4,773	5,893	6,869
6	0,718	0,906	1,134	1,440	1,943	2,447	3,143	3,707	4,317	5,208	5,959
7	0,711	0,896	1,119	1,415	1,895	2,365	2,998	3,499	4,029	4,785	5,408
8	0,706	0,889	1,108	1,397	1,860	2,306	2,896	3,355	3,833	4,501	5,041
9	0,703	0,883	1,100	1,383	1,833	2,262	2,821	3,250	3,690	4,297	4,781
10	0,700	0,879	1,093	1,372	1,812	2,228	2,764	3,169	3,581	4,144	4,587
11	0,697	0,876	1,088	1,363	1,796	2,201	2,718	3,106	3,497	4,025	4,437
12	0,695	0,873	1,083	1,356	1,782	2,179	2,681	3,055	3,428	3,930	4,318
13	0,694	0,870	1,079	1,350	1,771	2,160	2,650	3,012	3,372	3,852	4,221
14	0,692	0,868	1,076	1,345	1,761	2,145	2,624	2,977	3,326	3,787	4,140
15	0,691	0,866	1,074	1,341	1,753	2,131	2,602	2,947	3,286	3,733	4,073
16	0,690	0,865	1,071	1,337	1,746	2,120	2,583	2,921	3,252	3,686	4,015
17	0,689	0,863	1,069	1,333	1,740	2,110	2,567	2,898	3,222	3,646	3,965
18	0,688	0,862	1,067	1,330	1,734	2,101	2,552	2,878	3,197	3,610	3,922
19	0,688	0,861	1,066	1,328	1,729	2,093	2,539	2,861	3,174	3,579	3,883
20	0,687	0,860	1,064	1,325	1,725	2,086	2,528	2,845	3,153	3,552	3,850
21	0,686	0,859	1,063	1,323	1,721	2,080	2,518	2,831	3,135	3,527	3,819
22	0,686	0,858	1,061	1,321	1,717	2,074	2,508	2,819	3,119	3,505	3,792
23	0,685	0,858	1,060	1,319	1,714	2,069	2,500	2,807	3,104	3,485	3,767
24	0,685	0,857	1,059	1,318	1,711	2,064	2,492	2,797	3,091	3,467	3,745
25	0,684	0,856	1,058	1,316	1,708	2,060	2,485	2,787	3,078	3,450	3,725
26	0,684	0,856	1,058	1,315	1,706	2,056	2,479	2,779	3,067	3,435	3,707
27	0,684	0,855	1,057	1,314	1,703	2,052	2,473	2,771	3,057	3,421	3,690
28	0,683	0,855	1,056	1,313	1,701	2,048	2,467	2,763	3,047	3,408	3,674
29	0,683	0,854	1,055	1,311	1,699	2,045	2,462	2,756	3,038	3,396	3,659
30	0,683	0,854	1,055	1,310	1,697	2,042	2,457	2,750	3,030	3,385	3,646
40	0,681	0,851	1,050	1,303	1,684	2,021	2,423	2,704	2,971	3,307	3,551
50	0,679	0,849	1,047	1,299	1,676	2,009	2,403	2,678	2,937	3,261	3,496
60	0,679	0,848	1,045	1,296	1,671	2,000	2,390	2,660	2,915	3,232	3,460
80	0,678	0,846	1,043	1,292	1,664	1,990	2,374	2,639	2,887	3,195	3,416
100	0,677	0,845	1,042	1,290	1,660	1,984	2,364	2,626	2,871	3,174	3,390
120	0,677	0,845	1,041	1,289	1,658	1,980	2,358	2,617	2,860	3,160	3,373
∞	0,674	0,842	1,036	1,282	1,645	1,960	2,326	2,576	2,807	3,090	3,291

Remarque : la dernière ligne du tableau ci-dessus correspond aux grandes valeurs de k. Il s’agit d’un cas limite pour lequel la loi de Student est équivalente à la loi normale centrée et réduite.

Voir aussi

Notes et références

Bibliographie

• Gilbert Saporta, Probabilités, Analyse des données et Statistiques, Paris, Éditions Technip, 2006, 622 p. [détail des éditions] (ISBN 978-2-7108-0814-5, présentation en ligne)

Articles connexes

• Test de Student
• Erreur de mesure
• Fonction de Pearson
• Lemme de Scheffé

• Portail des probabilités et de la statistique