Nyquist–Shannonen laginketa teorema

Seinaleen prozesaketa digitalean, Nyquist-Shannonen laginketa teorema denbora jarraituko seinaleen eta denbora diskretuko seinaleen arteko lokarria da. Teoremak laginketa burutzean sortutako laginek denbora jarraituko seinalearen informazio guztia gorde dezaten laginketa maiztasunak bete beharreko baldintza ezartzen du. Teorema maiztasun banda mugatua duten seinale jarraituentzat baliagarria da soilik.

Sarrera

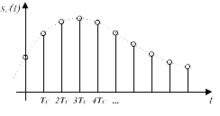
Lagintzea seinale jarraitu bat (soinua, ahotsa, tenperatura, tentsioa, irudiak… ) diskretu bihurtzea da, hau da, balio sekuentzia batera bihurtzea.

Laginketa prozesua honela adierazi daiteke: ${\displaystyle x(t)}$ denbora jarraituko seinale bat bada eta T_s laginketa periodoa (f_s=1/T_s, laginketa maiztasuna), lagindutako seinalea, ${\displaystyle x[n]}$, aldagai jarraituko seinalearen balioak une diskretuetan harturik (T_s tarterik behin) eraikitzen da. Adierazpen matematikoa hurrengoa da: ${\displaystyle x[n]=x(nT_{s})}$ non ${\displaystyle n\subset \mathbb {I} }$.

Claude E. Shannonek hurrengoa adierazi zuen:

${\displaystyle x(t)}$ funtzio batek ez badu B Hz-etik gorako maiztasunik, funtzioa guztiz zehaztu daiteke elkarrengandik ${\displaystyle 1/(2B)}$ segundo banaturik dauden puntuen koordenatuak adieraziz.^[1]

Aurrekoa kontuan hartuz, laginketa maiztasuna ${\displaystyle 2B}$ lagin/segundo baino altuagoa izan beharko da ${\displaystyle (f_{s}>2B)}$. ${\displaystyle 2B}$ lagin/segundo baino altuagoa den laginketa maiztasuna erabiliz gero, laginek jatorrizko seinalearen informazio nahikoa gordeko dute eta eraikitako seinale diskretuak jatorrizko seinalearen irudikapen zehatza eskainiko du. Era berean, ${\displaystyle f_{s}}$ laginketa maiztasun jakin baterako, seinalea perfektuki berreraikitzea posible dela bermatu daiteke, baldin eta seinaleak ${\displaystyle B<f_{s}/2}$ maiztasun muga badu.

${\displaystyle 2B}$ atariari Nyquisten abiadura deritzo eta ${\displaystyle x(t)}$ sarrera seinale jarraituaren ezaugarria da. Laginketa abiadura Nyquisten abiadura baino handiagoa izan behar da laginek ${\displaystyle x(t)}$ zehaztasunez irudikatzeko. ${\displaystyle f_{s}/2}$ atariari Nyquisten maiztasuna (${\displaystyle f_{N}}$) deritzo eta laginketa ekipoaren ezaugarria da. Ekipoak ${\displaystyle f_{s}}$ laginketa maiztasuna erabiliz kodetu dezakeen maiztasunik altuena da.

Shanonnek teorema denboraren mendeko seinale jarraituentzat formulatu bazuen ere, denbora domeinukoak ez diren beste funtzioei aplikatu ahal zaie, irudiei adibidez, espazio domeinuko funtzioei. Beste domeinu bateko seinaleekin lan egiten dugunean, t, f_s, eta Bren unitateak besterik ez dira aldatzen.

Aliasing

Nyquist-Shannonen laginketa teoremaren baldintza ez betetzeak aliasinga dakar ondorio gisa.

Aliasinga ulertzeko modurik errazena seinale sinusoidal puru baten laginketa aztertzea da. 3. irudian ikus daitekeen bezala, maiztasun ezberdineko bi seinale sinusoidalek laginketa puntu berberak partekatu ditzakete. Seinale sinusoidala ez bada behar adina altua den laginketa maiztasunarekin lagintzen, laginak erabiliz berreraikitako seinaleak iruditu dezake maiztasun baxuagoa duen beste seinale sinusoidal bat dela, hau da, alias bilakatuko da. Beste era batean esanda, eraikitako seinale diskretuak ez du jatorrizko seinalea irudikatuko.

Aliasingaren adierazpen matematikoari dagokionez, maiztasunaren eremuan garatu egiten da:

${\displaystyle X(f)}$, ${\displaystyle x(t)}$ funtzioaren Fourierren transformatua bada,

${\displaystyle X(f)\ \triangleq \ \int _{-\infty }^{\infty }x(t)\ e^{-i2\pi ft}\ {\rm {d}}t}$

lagindutako seinalearen Fourierren transformatua ${\displaystyle X_{s}(f)}$ hurrengo eran adierazi daiteke:

${\displaystyle X_{s}(f)\ \triangleq \sum _{k=-\infty }^{\infty }X\left(f-kf_{s}\right)}$

Ikus daitekeenez, ${\displaystyle X_{s}(f)}$ funtzio periodiko bat da, ${\displaystyle X(f)}$-ren kopiak ${\displaystyle f_{s}}$-ren multiploetara mugituz eta ondoren batuz eraikitzen dena. Lagindutako seinalearen maiztasun espektroa, beraz, jatorrizko seinalearen espektroaren kopiez osatuta egongo da, jatorrizko seinalearen espektroaren kopiak izango ditu ${\displaystyle f_{s}}$-ren multiplo guztietan. Maiztasun banda mugatuko ${\displaystyle (X(f)=0,\left\vert f_{s}\right\vert >B)}$ seinale bat eta ${\displaystyle f_{s}}$ balio egoki bat ${\displaystyle (f_{s}>2B)}$ baldin baditugu, posible da kopiak elkarrengandik banatuak mantentzea (4. irudia). Baina Nyquisten baldintza betetzen ez bada ${\displaystyle (f_{s}<2B)}$, elkarren ondoko kopiak gainjarri egiten dira. Kasu honetan, ${\displaystyle f_{s}/2}$ maiztasunetik gorako osagaiak ezin dira maiztasun baxuko osagaietatik bereizi, nahasirik agertzen dira ${\displaystyle f_{s}/2}$ maiztasunetik beherako osagaiekin. Horri aliasinga (alias: izen faltsua) deritzo. ${\displaystyle f_{s}/2}$ maiztasunetik gorako osagaiak alias bezala agertzen dira lagindutako seinalean, osagai jarraituaren (DC, f = 0 Hz) eta Nyquist maiztasunaren ${\displaystyle (f_{N}=f_{s}/2)}$ artean. Beste era batean esanda, ${\displaystyle f_{N}}$-tik gorako maiztasunak islaturik agertzen dira ${\displaystyle f_{N}}$-tik behera.

Batzuetan ez da posible nahi dugun laginketa maiztasuna erabiltzea, aurretik erabakia dago (industria estandarrak, esaterako). Kasu horietan, ${\displaystyle x(t)}$ iragazi egiten da laginketa burutu baino lehen. Iragazketa egiteko behe paseko iragazki bat erabiltzen da, anti-aliasing iragazkia deritzona. Anti-aliasing iragazkiaren ebaketa maiztasuna ${\displaystyle f_{s}/2}$ da, beraz, aliasak sortzen dituzten maiztasun osagaiak ezabatzen ditu. Anti-aliasing iragazkia erabiliz gero, goi maiztasunei buruzko informazioa galdu egiten da, ${\displaystyle f_{s}/2}$ maiztasunetik gorako maiztasun osagai guztiak ezabatu egiten baitira, baina ${\displaystyle f_{s}/2}$-tik beherakoak inolako distortsiorik gabe gorde daitezke. Anti-aliasing iragazkirik erabiliko ez bagenu, ${\displaystyle f_{s}/2}$ maiztasunetik gorako maiztasun osagaiei buruzko informazioa galduko litzateke, eta horrez gain, behe maiztasunei buruzkoa ere.

Teorema aldagai anitzeko seinaleetan

Laginketaren teorema aldagai bakarreko funtzioentzat formulatu ohi da normalean. Ondorioz, teorema denboraren mendeko seinaleetan aplikatu egiten da zuzenean eta testuinguru horretan formulatu egiten da. Hala ere, laginketa teorema aldagai anitzeko funtzioei aplikatu ahal zaie ere. Eskala griseko irudiak, adibidez, bi dimetsioko matrize bezala adierazten dira normalean. Matrizeko zenbakiek dagokien zutabe eta lerro elkarguneko pixelen intentsitatea adierazten dute. Beraz, irudiek bi aldagai independente behar dituzte pixel bakoitza adierazteko, bata lerroa zehazteko eta bestea zutabea zehazteko.

Kolorezko irudiak hiru dimentsioko matrizez eraikita daude, dimentsio bakoitzak oinarrizko kolore bat adierazten duelarik: gorria, berdea eta urdina (RGB). Badaude hiru dimentsioko beste kolore espazio batzuk: HSV, CIELAB, XYZ…. Lau dimentsioko kolore espazioak ere existitzen dira, CMYK esaterako. Horiek guztiak aldagai anitzeko funtzioak dira.

Nyquisten teorema kamera sistemei ere aplikatu ahal zaie. Sistema horietan paisaia eta kameraren lentea seinale analogiko espazialaren iturriak dira eta irudi sentsorea laginketa espaziala burutzen duen gailua da. Dimentsio bakarreko seinale diskretuen kasuan bezalaxe, irudiek aliasinga izan dezakete laginketa bereizmena egokia ez bada, hau da, ez badira pixel nahikoa erabiltzen irudia irudikatzeko. Aliasingaren adibidea ikusi dezakegu 6. irudian, laginketa teoremaren baldintza bete ez denean lortutako irudia ikus daiteke. Aliasinga moiré patroi bezala agertzen da. 7. irudian aliasingik gabeko irudia ikus daiteke.

Espazio domeinuan, laginketa handiagoa lortzeko “konponbidea” argiazkia atera nahi den objektutik hurbilago kokatzea, bereizmen handiagoko sentsore bat erabiltzea edo laginketa burutu baino lehen irudia lausotzea izango litzateke.

Teoremaren jatorria

Teoremaren izenak Harry Nyquist eta Claude E. Shannon ondratzen dituen arren, beste teorialari eta matematikari batzuek ere teorema “aurkitu” zuten independenteki. V. A. Kotelnikov teorialariak Shannonen antzeko emaitzak argitaratu zituen 1933an. Izan ere, 1999an Eduard Rhein Fundazioak Kotelnikov saritu zuen "laginketa teoremaren lehenengo azalpen teoriko zehatzagatik". E.T. Whittaker matematikariak laginketa teorema azaldu zuen ere 1915ean. Izatez, Whittakerrek 1915ean argitaraturiko lana laginketaren teorema banda mugatuko funtzioentzat azaltzen duen lehenengo lana da.

Harry Nyquisti dagokionez, 1928an azaldu zuen teorema lehenengoz. Nyquistek ez zuen teorema esplizituki azaldu, baina inplizituki agertzen zen 1928an argitaraturiko lanean. Lan horretan, Nyquistek 2B banda zabalerako pultsuak B banda zabalerako sistema batetik bidali zitezkeela adierazi zuen, baina ez zituen seinale jarraien laginketa eta berreraikitzea esplizituki kontsideratu. Claude E. Shannon matematikaria izan zen teorema forgatu zuena 1949an.

Teorema pertsona ezberdinei egotzi egiten zaie, hori dela dela, teorema Nyquist–Shannon–Kotelnikov, Whittaker–Shannon–Kotelnikov edo Whittaker–Nyquist–Kotelnikov–Shannon gisa ezagutzen da ere.

Erreferentziak

Bibliografia

• Shannon, C.E.. (1949-1). «Communication in the Presence of Noise» Proceedings of the IRE 37 (1): 10–21.  doi:10.1109/JRPROC.1949.232969. ISSN 0096-8390. (Noiz kontsultatua: 2019-10-26).
• (Ingelesez) Whittaker, E. T.. (1915). «XVIII.—On the Functions which are represented by the Expansions of the Interpolation-Theory» Proceedings of the Royal Society of Edinburgh 35: 181–194.  doi:10.1017/S0370164600017806. ISSN 0370-1646. (Noiz kontsultatua: 2019-11-14).
• Nyquist, H.. (1928-4). «Certain Topics in Telegraph Transmission Theory» Transactions of the American Institute of Electrical Engineers 47 (2): 617–644.  doi:10.1109/T-AIEE.1928.5055024. ISSN 0096-3860. (Noiz kontsultatua: 2019-11-14).
• Sarrera analogikoa, http://www.ehu.eus/instru_virtualdaq/atal_3/atal_3.htm

Ikus, gainera

• Fourierren transformatua
• Ahotsa digitalizatzeko teknikak

Kanpo estekak

• Signal Sampling: Nyquist - Shannon Theorem Applet

• Datuak: Q679800
• Multimedia: Nyquist Shannon theorem / Q679800