Trajetória ortogonal

Uma equação da forma ${\displaystyle f(x,y)=c}$, onde ${\displaystyle c}$ é uma constante, define uma família de curvas. As trajetórias ortogonais são outra família de curvas que intersetam a primeira família em forma ortogonal: em cada ponto de uma das curvas da primeira família passa uma curva da segunda família, formando um ângulo de 90${\displaystyle ^{\circ }}$.^[1]

Para encontrar a família de trajetórias ortogonais às curvas ${\displaystyle f(x,y)=c}$, é necessário encontrar uma equação diferencial cuja solução geral seja ${\displaystyle f(x,y)=c}$; essa equação encontra-se derivando implicitamente a equação anterior.

${\displaystyle {\partial f \over \partial x}+{\dfrac {\partial f}{\partial y}}{dy \over dx}=0\qquad \Longrightarrow \qquad {dy \over dx}=-}$ ${\displaystyle {\dfrac {\partial f}{\partial x}} \over {\dfrac {\partial f}{\partial y}}}$

A derivada ${\displaystyle dy/dx}$ representa em cada ponto o declive da curva que passa por esse ponto. O declive da curva ortogonal será o inverso, com sinal trocado

${\displaystyle {dy \over dx}=}$${\displaystyle {\dfrac {\partial f}{\partial y}} \over {\dfrac {\partial f}{\partial x}}}$

a solução geral desta equação é a família de trajetórias ortogonais.^[1]

Exemplo

Encontre as trajetórias ortogonais da família de círculos com centro na origem.^[1]

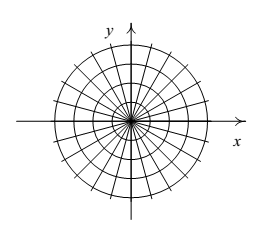
A equação dos círculos com centro na origem é

${\displaystyle x^{2}+y^{2}=c^{2}}$

onde o parâmetro ${\displaystyle c}$ pode ter qualquer valor positivo a equação diferencial cuja solução geral é essa família de círculos obtém-se por derivação implícita

${\displaystyle 2x+2yy'=0\qquad \Longrightarrow \qquad {dy \over dx}=-{x \over y}}$

e a equação diferencial das trajetórias ortogonais é

${\displaystyle {dy \over dx}={\frac {y}{x}}}$

A solução desta equação de variáveis separáveis é

${\displaystyle y=ax}$

que corresponde a uma família de retas que passam pela origem; a constante de integração é declive das retas. A figura mostra a família de curvas e as trajetórias ortogonais.^[1]

Referências

Ver também

• Equação diferencial
• Equação diferencial linear
• Equação diferencial de Bernoulli

Este artigo sobre matemática é um esboço. Você pode ajudar a Wikipédia expandindo-o. v d e

• Portal da matemática