Rozkład Laplace’a

Rozkład Laplace’a
Gęstość prawdopodobieństwa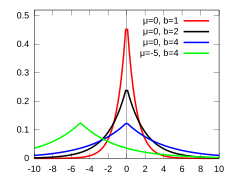
Ilustracja
Dystrybuanta
Ilustracja
Parametry

μ ∈ R {\displaystyle \mu \in \mathbb {R} } wartość średnia b > 0 {\displaystyle b>0} parametru skali

Nośnik

R {\displaystyle \mathbb {R} }

Gęstość prawdopodobieństwa

1 2 b exp ⁡ ( − | x − μ | b ) {\displaystyle {\frac {1}{2b}}\exp \left(-{\frac {|x-\mu |}{b}}\right)}

Dystrybuanta

{ 1 2 exp ⁡ ( x − μ b ) dla  x ⩽ μ 1 − 1 2 exp ⁡ ( − x − μ b ) dla  x ⩾ μ {\displaystyle {\begin{cases}{\frac {1}{2}}\exp \left({\frac {x-\mu }{b}}\right)&{\text{dla }}x\leqslant \mu \\[8pt]1-{\frac {1}{2}}\exp \left(-{\frac {x-\mu }{b}}\right)&{\text{dla }}x\geqslant \mu \end{cases}}}

Wartość oczekiwana (średnia)

μ {\displaystyle \mu }

Mediana

μ {\displaystyle \mu }

Moda

μ {\displaystyle \mu }

Wariancja

2 b 2 {\displaystyle 2b^{2}}

Współczynnik skośności

0 {\displaystyle 0}

Kurtoza

3 {\displaystyle 3}

Entropia

ln ⁡ ( 2 b e ) {\displaystyle \ln(2be)}

Funkcja tworząca momenty

exp ⁡ ( μ t ) 1 − b 2 t 2  dla  | t | < 1 / b {\displaystyle {\frac {\exp(\mu t)}{1-b^{2}t^{2}}}{\text{ dla }}|t|<1/b}

Funkcja charakterystyczna

exp ⁡ ( μ i t ) 1 + b 2 t 2 {\displaystyle {\frac {\exp(\mu it)}{1+b^{2}t^{2}}}}

Odkrywca

Pierre Simon de Laplace

Rozkład Laplace’a – ciągły rozkład prawdopodobieństwa nazwany na cześć Pierre’a Laplace’a.

Rozkład Laplace’a nazywany jest także czasem dwustronnym rozkładem wykładniczym, gdyż powstaje podczas odejmowania dwóch rozkładów wykładniczych. Ściślej mówiąc, jeśli X 1 , X 2 {\displaystyle X_{1},X_{2}} są niezależnymi zmiennymi losowymi o rozkładzie wykładniczym z parametrem λ = 1 / b , {\displaystyle \lambda =1/b,} to zmienna losowa

μ + X 1 − X 2 {\displaystyle \mu +X_{1}-X_{2}}

ma rozkład Laplace’a o średniej μ {\displaystyle \mu } i czynniku skali b {\displaystyle b} [1].

Rozkład Laplace’a powstaje także, kiedy mnożymy zmienną o rozkładzie wykładniczym przez losowy znak. Dokładniej, jeśli X {\displaystyle X} ma rozkład wykładniczy z parametrem λ = 1 / b , {\displaystyle \lambda =1/b,} a Y {\displaystyle Y} ma rozkład jednostajny na zbiorze { − 1 , 1 } {\displaystyle \{-1,1\}} oraz zmienne X , Y {\displaystyle X,Y} są niezależne, to zmienna X Y {\displaystyle XY} ma rozkład Laplace’a o średniej 0 {\displaystyle 0} i skali b {\displaystyle b} [2].

Zobacz też

Przypisy

Bibliografia

  • Rozkład Laplace’a. Michiel Hazewinkel (red.). w: Encyclopaedia of Mathematics Kluwer Academic Publishers, 2001. ISBN 978-1556080104. (ang.).
  • Wojciech Niemiro, Symulacje stochastyczne i metody Monte Carlo, Uniwersytet Warszawski.