Student'in t dağılımı

Student'in t

Olasılık yoğunluk fonksiyonu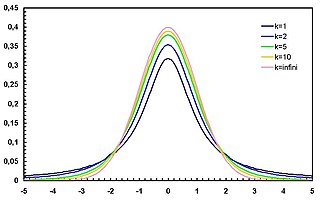
Yığmalı dağılım fonksiyonu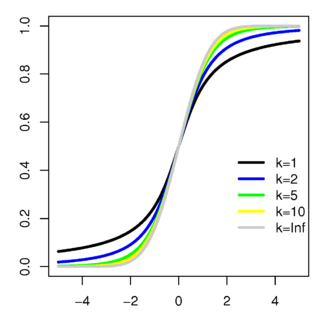
Parametreler	${\displaystyle \nu >0}$ serbestlik dereceleri (reel)
Destek	${\displaystyle x\in (-\infty ;+\infty )\!}$
Olasılık yoğunluk fonksiyonu (OYF)	${\displaystyle {\frac {\Gamma ({\frac {\nu +1}{2}})}{{\sqrt {\nu \pi }}\,\Gamma ({\frac {\nu }{2}})}}\left(1+{\frac {x^{2}}{\nu }}\right)^{-({\frac {\nu +1}{2}})}\!}$
Birikimli dağılım fonksiyonu (YDF)	${\displaystyle {\begin{matrix}{\frac {1}{2}}+x\Gamma \left({\frac {\nu +1}{2}}\right)\cdot \\[0.5em]{\frac {\,_{2}F_{1}\left({\frac {1}{2}},{\frac {\nu +1}{2}};{\frac {3}{2}};-{\frac {x^{2}}{\nu }}\right)}{{\sqrt {\pi \nu }}\,\Gamma ({\frac {\nu }{2}})}}\end{matrix}}}$ burada ${\displaystyle \,_{2}F_{1}}$birhipergeometrik fonksiyon olur
Ortalama	${\displaystyle 0{\text{ eğer }}\nu >1}$, diğer hallerde tanımlanmamış
Medyan	${\displaystyle 0}$
Mod	${\displaystyle 0}$
Varyans	${\displaystyle {\frac {\nu }{\nu -2}}{\text{ eğer }}\nu >2\!}$, diğer hallerde tanımlanmamış
Çarpıklık	${\displaystyle 0{\text{ for }}\nu >3}$
Fazladan basıklık	${\displaystyle {\frac {6}{\nu -4}}{\text{ for }}\nu >4\!}$
Entropi	${\displaystyle {\begin{matrix}{\frac {\nu +1}{2}}\left[\psi ({\frac {1+\nu }{2}})-\psi ({\frac {\nu }{2}})\right]\\[0.5em]+\log {\left[{\sqrt {\nu }}B({\frac {\nu }{2}},{\frac {1}{2}})\right]}\end{matrix}}}$ ${\displaystyle \psi }$: digamma fonksiyonu, ${\displaystyle B}$: beta fonksiyonu
Moment üreten fonksiyon (mf)	()
Karakteristik fonksiyon

Olasılık kuramı ve istatistik bilim dallarında t-dağılımı ya da Student'in t dağılımı genel olarak örneklem sayısı veya sayıları küçük ise ve anakütle normal dağılım gösterdiği varsayılırsa çıkartımsal istatistik uygulaması için çok kullanılan bir sürekli olasılık dağılımıdır. Çok popüler olarak tek bir anakütle ortalaması için güven aralığı veya hipotez sınaması ve iki anakütle ortalamasının arasındaki fark için güven aralığı veya hipotez sınamasında, yani çıkarımsal istatistik analizlerde, uygulama görmektedir.

t-dağılımı ilk olarak 1908'de Dublin'de Guinness Bira Fabrikası'nda çalışan William Sealy Gosset tarafından yayımlanan bir makale ile ortaya konmuştur. Guinness'in, şirket sırlarının yayımlanmasını önlemek amacıyla çalışanlarının bilimsel yayın yapmasını yasaklamasından ötürü, bu yayının yazarı Student (öğrenci) olarak belirtilmişti. Gosset bu makalesinde "t" yerine "z" harfini kullanmıştır fakat sonradan "z" harfinin standart normal dağılım bağlamında kullanılmaya başlanmasıyla Student'in dağılımı "t" harfiyle anılmaya başlanmıştır.^[1] t-sınamaları ve ilişkili teori R.A. Fisher tarafından geliştirilmiş ve bu dağılım Student'in t dağılımı adıyla tanınmıştır.

Çıkarımsal istatistiksel çalışmalarda normal dağılımın yerine küçük orneklem bulunan problemler için kullanılmakla (ve bu nedenle normal dağılımın bir özel hali olarak yanlış intiba vermekle) beraber Student'in t-dağılımı teorik bakımdan genelleştirilmiş hiperbolik dağılımının bir özel halidir.

Farz edelim ki X₁, ..., X_n istatistiksel olarak birbirlerinden bağımsız rassal değişkenlerdir ve beklenen değer μ ile dağılma σ değerleri ile normal dağılmaktadırlar.

${\displaystyle {\overline {X}}_{n}=(X_{1}+\cdots +X_{n})/n}$

örneklem ortalaması ve

${\displaystyle S_{n}^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}\left(X_{i}-{\overline {X}}_{n}\right)^{2}}$

Bu Z den, kesin standart sapma ifadesi olan ${\displaystyle \scriptstyle \sigma }$ yerine bir rassal değişken olan ${\displaystyle \scriptstyle S_{n}}$ konulması suretiyle değişiklik gösterir. Teknik olarak :${\displaystyle \scriptstyle (n-1)S_{n}^{2}/\sigma ^{2}}$ Cochran'ın teoremine göre bir ki-kare dağılımı gösterir. Gosset yazısında Tnin şu olasılık yoğunluk fonksiyonu gösterdiğini ispat etmiştir:

${\displaystyle f(t)={\frac {\Gamma ({\frac {\nu +1}{2}})}{{\sqrt {\nu \pi }}\,\Gamma ({\frac {\nu }{2}})}}\left(1+{\frac {t^{2}}{\nu }}\right)^{-({\frac {\nu +1}{2}})}\!,}$

Burada ν, n - 1 ifadesine eşittir ve Γ bir Gamma fonksiyonudur.

Bu ifade şöyle de yazılabilir:

${\displaystyle f(t)={\frac {1}{{\sqrt {\nu }}\,B\left({\frac {1}{2}},{\frac {\nu }{2}}\right)}}\left(1+{\frac {t^{2}}{\nu }}\right)^{-({\frac {\nu +1}{2}})}\!,}$

Burada B bir Beta fonksiyonudur.

Sonradan T dağılımı t-dağılımı olarak anılmaya başlanmıştır. ν parametresi serbestlik derecesi olarak anılmaktadır. Dikkat edilirse t-dağılımı sadece ν parametresine dayanır ve (çıkarımsal istatistik analizi için bilinmeyen anakütle değerleri olan) μ veya σ t-dağılımı için parametre değildirler. İşte bu gerçek (yani μ ve σ nin parametre olmaması) hem teorik bakımdan ve daha belirgin olarak pratik çıkarımsal istatistik analizi bakımından, t-dağılımı istatistik bilimi için çok önemlidir.

t-dağılımının momentleri şunlardır:

${\displaystyle E(T^{k})={\begin{cases}0&{\mbox{k tek}},\quad 0<k<\nu \\{\frac {\Gamma ({\frac {k+1}{2}})\Gamma ({\frac {\nu -k}{2}})\nu ^{k/2}}{{\sqrt {\pi }}\Gamma ({\frac {\nu }{2}})}}&{\mbox{k cift}},\quad 0<k<\nu \\{\mbox{NaN}}&{\mbox{k tek}},\quad 0<\nu \leq k\\\infty &{\mbox{k cift}},\quad 0<\nu \leq k\\\end{cases}}}$

Bir diğer işlemle de 0 < k < ν terimi, k çift sayı ise, Gamma fonksiyonunun özellikleri kullanılarak daha basitleştirilebilinir:

${\displaystyle E(T^{k})=\prod _{i=1}^{k/2}{\frac {2i-1}{\nu -2i}}\nu ^{k/2}\qquad k{\mbox{ cift}},\quad 0<k<\nu .}$

Daha ileri teori

Gosset'in sonuçlarının daha da genelleştirilmesi mümkündür.^[2]

Z, standart normal dağılıma ve V ise, ${\displaystyle \nu }$ serbestlik derecesi ile ki-kare dağılımına sahip olsun, Z ve V bağımsız ise, Cochran'in teoremine göre, şu orantı

${\displaystyle {\frac {Z}{\sqrt {V/\nu \ }}}}$

ν serbestlik derecesi olan bir t-dağılımı olur.

Serbestlik derecesi ν olan bir t-dağılımı için beklenen değer 0 dır ve varyans

ν/(ν - 2) eğer ν > 2.

Çarpıklık 0 olur ve basıklık eğer ν > 4 ise.

6/(ν - 4)

olur. Yığmalı dağılım fonksiyonu bir tamamlanmamış beta fonkiyonu olup

${\displaystyle \int _{-\infty }^{t}f(u)\,du=I_{x}\left({\frac {\nu }{2}},{\frac {\nu }{2}}\right)}$

ifadesi ile verilir ve burada

${\displaystyle x={\frac {t+{\sqrt {t^{2}+\nu }}}{2{\sqrt {t^{2}+\nu }}}}.}$

olur.

t-dağılımı ile F-dağılımı ilişkisi şöyle açıklanabilir; ν serbestlik derecesi olan t için kare değeri serbestlik derecesi 1 ve ν olan bir F-dağılımıdır.

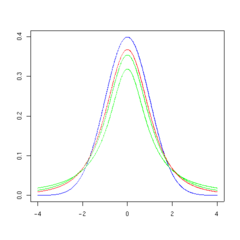
t-dağılımının olasılık yoğunluk fonksiyonunu grafik şekli, ortalaması 0 ve varyansı 1 olan standart normal dağılımı grafik şekline benzerlik gösterir. Ancak t-dağılımı daha yaygındır ve biraz daha basıktır. Serbestlik derecesi büyüdükçe, t-dağılımı standart normal dağılımına yaklaşım göstermektedir. Serbestlik derecesi 30 olduğu zaman t-dağılımı ve standart normal dağılım nerede ise aynı şekildedirler.

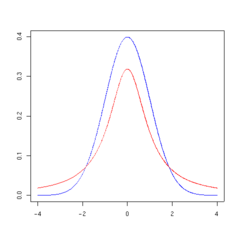
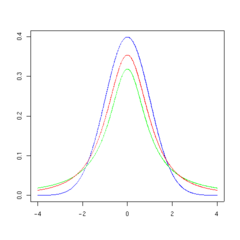
Aşağıdaki gösterimler ν serbestlik derecesi artış gösterirse t-dağılımı yoğunluk fonksiyonunun nasıl değiştiğini gösterirler. Karşılaştırma sağlamak için normal dağılım mavi çizgi ile gösterilmiştir. t-dağılımını gösteren kırmızı çizginin ν değeri artıkça normal dağılıma yakınlaşma gösterdiği açıkça gözlenebilmektedir. Eğer ν=30 t-dağılımı hemen hemen normal dağılım ile aynı olmaktadır.

Serbestlik dereceleri 1, 2, 3, 5, 10 ve 30 için t-dağılımı yoğunluk fonksiyonu (kırmızı ve yeşil). Normal dağılımla (mavi) karşılaştırın.

Özel haller

Serbestlik derecesini ν için belli değerler özellikle basit olan bazı şekilleri verirler:

ν = 1

Dağılım fonksiyonu şu olur:

${\displaystyle F(x)={\frac {1}{2}}+{\frac {1}{\pi }}\arctan(x).}$

Yoğunluk fonksiyonu şudur:

${\displaystyle f(x)={\frac {1}{{\pi }(1+x^{2})}}.}$

Bakın Cauchy dağılımı

ν = 2

Dağılım fonksiyonu şu olur:

${\displaystyle F(x)={\frac {1}{2}}\left[1+{\frac {x}{\sqrt {2+x^{2}}}}\right].}$

Yoğunluk fonksiyonu şudur:

${\displaystyle f(x)={\frac {1}{\left(2+x^{2}\right)^{3/2}}}.}$

Student'in t-dağılımı kullanarak kestirim aralığı bulunması

Bir sayı olan A öyle şekilde seçilsin ki

${\displaystyle \Pr(-A<T<A)=0.9,\,}$

olsun. Burada T n - 1 serbestlik derecesi bulunan bir t-dağılımı göstersin. Bu ifade

${\displaystyle \Pr(T<A)=0.95,\,}$

ifadesi ile aynı olup A bu olasılık dağılımının 95inci yüzdebirlik değeridir veya

${\displaystyle A=t_{(0.05,n-1)}}$.

Bu halde

${\displaystyle \Pr \left(-A<{{\overline {X}}_{n}-\mu \over S_{n}/{\sqrt {n}}}<A\right)=0.9,}$

olmaktadır ve bu da

${\displaystyle \Pr \left({\overline {X}}_{n}-A{S_{n} \over {\sqrt {n}}}<\mu <{\overline {X}}_{n}+A{S_{n} \over {\sqrt {n}}}\right)=0.9.}$

ifadesine aynen eşittir. Bunun için uç-noktaları

${\displaystyle {\overline {X}}_{n}\pm A{\frac {S_{n}}{\sqrt {n}}}}$

olan açıklık μ için bir %90 güven aralığıdır.

Böylece eğer normal dağılım gösterdiğine epeyce emin olabilaceğimiz bir grup gözlem için ortalama değeri bulursak, t-dağılımını kullanarak bulunan ortalama için güvenlik limitlerinin (belki bir sıfır hipotez için tahmin edilmiş değerin) yahut daha önce teorik olarak tahmin edilmiş bir değerin, bu limitlerin arasında bulunup bulunmadığı araştırılabilir.

Bu sonuc Student'in t-testlerinde kullanılmaktadır. İki normal dağılımdan alınan örneklemlerin ortalamalarının farkı da normal dağılım gösterdiği için, anakütle ortalamalarının arasındaki farkın sıfıra eşit olduğuna dair bir sonuç çıkarmanın makul olup olmadığını incelemede kullanılabilir.

Eğer veriler normal olarak dağılım gösterirlerse, ortalama için tek taraflı bir (1-a)-üst güvenlik limiti (UGL), şu verilen denklemi kullanarak hesaplanabilir.

${\displaystyle \mathrm {UGL} _{1-a}={\overline {X}}_{n}+{\frac {t_{a,n-1}S_{n}}{\sqrt {n}}}.}$

Ortaya çıkarılan UGL değeri, bir verilmiş güvenlik aralığı ve anakütle büyüklüğü için ortaya çıkacak en büyük ortalama değeri olacaktır. Diğer bir terimle, ${\displaystyle {\overline {X}}_{n}}$ değeri bir grup gözlemler için bir ortalama olursa, bu dağılımın ortalamasının ${\displaystyle \mathrm {UCL} _{1-a}}$ değerinden daha düşük olmasının olasılığı güvenlik oranına (yani ${\displaystyle 1-a}$ ye) eşittir.

Uygun büyüklükteki örneklemler için t-dağılımlarının ilgili sıfır hipotezi için uygulanabileceği birkaç diğer istatistikler bulunmaktadır. Böylece t-dagılımı, yalnizca tek ortalama ve iki ortalama arasındaki fark problemleri için uygulanan sonuç verici istatistik için bir özel teknik olmadığı açıktır. Örneğin Spearman'ın sıralama korelasyon katsayısı için sıfır hipotez bu katsayının 0 olabileceği ise, bu sıfır korelasyon için, eğer örneklem büyüklüğü 20 civarında ise, yaklaşık olarak bir t-dağılımı kullanılabilir.

Güçlü parametrik modelleme

t-dağılımı çok kere veri modeli kurmak için normal dağılıma bir alternatif olarak kullanılır. Çok kere pratik hayattan gelen gerçek veriler normal dağılımın kabul ettiğinden daha fazla ağırlıklı dağılım (şişman-kuyruklu dağılım) gösterir. Bu halde klasik çözum yolu bu alışılanın çok dışında olan değerleri (aykırı değerleri) teşhis edip bunların ağırlıklarını özel işlemlerle azaltmaya çaba göstermekle yapılmaktaydı. Ancak aykırı değerlerin teşhis edilmesi (özellikle yüksek boyut gösteren veriler arasında) hiç kolay olmamaktadır. Bu nedenle bu türlü verileri modellemek için doğasal seçim konusu olan ve güçlü istatistikler için bir parametrik yaklaşım sağlayan t-dağılımının alternatif olarak kullanılması tavsiye edilmektedir.

Lange ve işbirlikçileri (1989) ^[3] çeşitli kullanım alanlarında sisman kuyruklu veriler için güçlü modelleme içinde t-dağılımının kullanılması sorunu ayrıntılı olarak incelemişlerdir. Gelman ve işbirlikçilerinin (2003) ^[4] yazısında bir Bayes-tipi yaklaşım gösterilmektedir. Serbestlik derecesi parametresi dağılımının basıklığını kontrol etmek için kullanılmakta ve bu ölçek parametresi ile korelasyon bağlantısı göstermektedir. Olabilirlilik çok sayıda yerel maksimum değerleri gösterdiği için, çok kere serbestlik derecesini ufak olan değerlerde sabitleştirmek ve bu sabit değer verilmiş gibi diğer parametreler için kestirimde bulunmak gerekmektedir. Bazı araştırıcılar bunun için en uygun değerlerin 3 ile 9 arasında olduğunu beyan etmişlerdir. Venebale ve Ripley (2002) ^[5] ise 5 değerinin iyi bir seçim olacağını bildirmektedirler.

İlişkili dağılımlar

• Eğer ${\displaystyle \sigma ^{2}\sim {\mbox{Inv-}}\chi ^{2}(\nu ,1)\!}$ bir ölçeği değişmiş ters-χ² dağılımı ve ${\displaystyle X\sim \mathrm {N} (0,\sigma ^{2})\!}$ ise bir normal dağılım gösteriyorlarsa, o halde ${\displaystyle X\sim \mathrm {t} (\nu )}$ bir t-dağılımı gösterir.
• Eğer ${\displaystyle Y=X^{2}\!}$ ve ${\displaystyle X\sim \mathrm {t} (\nu )\!}$ Student'in t-dağılımı gösteriyorlarsa ${\displaystyle Y\sim \mathrm {F} (\nu _{1}=1,\nu _{2}=\nu )}$ ifadesi bir F-dağılımı gösterir.
• ${\displaystyle X\sim \mathrm {t} (\nu )}$ iken ${\displaystyle Y=\lim _{\nu \to \infty }X}$ ise ${\displaystyle Y\sim \mathrm {N} (0,1)\!}$ bir normal dağılımı gösterir.
• Eğer ${\displaystyle X\sim \mathrm {t} (\nu =1)}$ ise ${\displaystyle X\sim \mathrm {Cauchy} (0,1)}$ bir Cauchy dağılımı gösterir.

Ayrıca bakınız

• Student'in t-testi
• Gamma fonksiyonu
• Hotelling'in T-kare dağılımı
• Merkezsel olmayan t-dağılımı
• Çokdeğişirli Student dağılımı
• Güven aralıkları

Kaynakça

Diğer

• Student [William Sealy Gosset] (Mart 1908). "The probable error of a mean" (PDF). Biometrika. 6 (1). ss. 1-25. 8 Mart 2008 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 4 Mart 2008. 
• Fisher, R. A. (1925). "Applications of "Student's" distribution" (PDF). Metron. Cilt 5. ss. 90-104. 13 Nisan 2011 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 4 Mart 2008. 
• Lange, K.L. (1989). "Robust Statistical Modeling Using the t Distribution". Journal of the American Statistical Association. Cilt 84. ss. 881-896. 
• Hogg, R.V. (1978). Introduction to Mathematical Statistics. New York: Macmillan. 
• Press, William H. (1992). Numerical Recipes in C: The Art of Scientific Computing. Cambridge University Press. 0-521-43108-5. 
• Venables, W.N. (2002). Modern Applied Statistics with S (Fourth Edition). Springer. 
• Gelman, Andrew (2003). Bayesian Data Analysis (Second Edition). CRC/Chapman & Hall. 1-584-88388-X. 

Dış bağlantılar

• VassarStats Kullanıcı tarafından belirtilen serbestlik derecesi için yoğunluk grafiği, kritik değerler vb.
• Earliest Known Uses of Some of the Words of Mathematics3 Ekim 1999 tarihinde Wayback Machine sitesinde arşivlendi. ("Student'in dağılımı" teriminin tarihi üzerine bazı görüşler)
• Student'in t-dağılımı için yığmalı yoğunluk fonksiyonu hesaplayıcısı
• Student'in t-dağılımı için olasılık yoğunluk fonksiyonu hesaplayıcısı