Teorema das cascas esféricas

Na mecânica clássica, o teorema das cascas esféricas provê importantes simplificações no cálculo do campo gravitacional de corpos com simetria esférica. Este Teorema foi provado por Isaac Newton, aos 23 anos, através do uso do Cálculo Diferencial e Integral, o qual ele mesmo desenvolveu. O teorema afirma que:

  • Um corpo com simetria esférica afeta objetos externos como se toda a sua massa estivesse concentrada em um único ponto no seu centro;
  • Uma casca com simetria esférica (esfera oca) não exerce força gravitacional no seu interior.

Um corolário dessas duas afirmações é:

  • Dentro de uma esfera sólida de densidade constante, a força gravitacional varia linearmente com a distância até o centro e anula-se nele.

Fora de uma esfera oca

Uma esfera oca pode ser vista como uma soma de anéis de espessura "dθ" e raio "R sen θ".

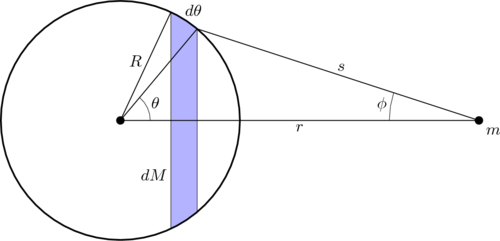
A força exercida no ponto "m" pode ser calculada integrando a força gravitacional de todas as secções.

A força gravitacional exercida pela secção sombreada é dado por:

d F = G m d M s 2 . {\displaystyle dF={\frac {Gm\;dM}{s^{2}}}.}

Contudo, pode observar-se pela simetria do problema que todas as componentes vectorias anulam-se excepto:

d F r = G m d M s 2 cos ⁡ ϕ . {\displaystyle dF_{r}={\frac {Gm\;dM}{s^{2}}}\cos \phi .}

Integrando:

F r = ∫ d F r = G m ∫ d M cos ⁡ ϕ s 2 . {\displaystyle F_{r}=\int dF_{r}=Gm\int {\frac {dM\cos \phi }{s^{2}}}.}

Para se expandir "dM" em função de "dθ", note-se que a área total da esfera é:

4 π R 2 {\displaystyle 4\pi R^{2}\,}

e a superfícies de secção entre "θ" e "dθ" tem área :

2 π R 2 sin ⁡ θ d θ {\displaystyle 2\pi R^{2}\sin \theta \,d\theta }

Portanto:

d M = 2 π R 2 sin ⁡ θ 4 π R 2 M d θ = 1 2 M sin ⁡ θ d θ {\displaystyle dM={\frac {2\pi R^{2}\sin \theta }{4\pi R^{2}}}M\,d\theta =\textstyle {\frac {1}{2}}M\sin \theta \,d\theta }

Logo:

F r = G M m 2 ∫ sin ⁡ θ cos ⁡ ϕ s 2 d θ {\displaystyle F_{r}={\frac {GMm}{2}}\int {\frac {\sin \theta \cos \phi }{s^{2}}}\,d\theta }

Relembrando a Lei dos cossenos:

cos ⁡ ϕ = r 2 + s 2 − R 2 2 r s {\displaystyle \cos \phi ={\frac {r^{2}+s^{2}-R^{2}}{2rs}}}
cos ⁡ θ = r 2 + R 2 − s 2 2 r R . {\displaystyle \cos \theta ={\frac {r^{2}+R^{2}-s^{2}}{2rR}}.}

A diferenciação da função implícita:

sin ⁡ θ d θ = s r R d s . {\displaystyle \sin \theta \;d\theta ={\frac {s}{rR}}ds.}

Obtém-se então:

F r = G M m 2 r R ∫ cos ⁡ ϕ s d s {\displaystyle F_{r}={\frac {GMm}{2rR}}\int {\frac {\cos \phi }{s}}\,ds}

Em que "s" varia de "r" - "R" ate "r" + "R".

Inserido a segunda expressão acima da "lei dos cossenos":

F r = G M m 4 r 2 R ∫ ( 1 + r 2 − R 2 s 2 ) d s . {\displaystyle F_{r}={\frac {GMm}{4r^{2}R}}\int \left(1+{\frac {r^{2}-R^{2}}{s^{2}}}\right)ds.}

A primitiva do integrando é:

s − r 2 − R 2 s {\displaystyle s-{\frac {r^{2}-R^{2}}{s}}}

e integrando entre r - R , r + R:

F r = G M m r 2 . {\displaystyle F_{r}={\frac {GMm}{r^{2}}}.}

Resultado equivalente a força gravitacional de um único ponto no centro.

Dentro de uma esfera oca

Pode ver-se que s varia de "R" - "r" ate "R" + "r". Utilizando a primitiva obtida anteriormente:

s − r 2 − R 2 s {\displaystyle s-{\frac {r^{2}-R^{2}}{s}}}

obtém-se:

F r = 0 {\displaystyle F_{r}=0\,}

ou seja, uma casca com simetria esférica (esfera oca) não exerce força gravitacional no seu interior.

Referências

  • Haliday, Resnick e Merril (1994). LTC, ed. Fundamentos de Física 2 3a ed. [S.l.: s.n.] 
  • Portal da física