Teoria delle rappresentazioni

La teoria delle rappresentazioni è una branca della matematica che studia le strutture algebriche astratte "rappresentando" i loro elementi come trasformazioni lineari di spazi vettoriali^[1] e studiando i moduli su queste strutture algebriche astratte.^[2] Sostanzialmente una rappresentazione rende più concreto un oggetto algebrico astratto descrivendo i suoi elementi mediante matrici. La teoria delle matrici e delle trasformazioni lineari è ben nota, quindi rappresentazioni di oggetti più astratti in termini di oggetti familiari dell'algebra lineare semplifica i calcoli e aiuta a capire e determinare le proprietà di questi oggetti astratti.

Un gruppo di Lie è un gruppo che è anche una varietà differenziabile. Molti gruppi classici di matrici sui numeri reali o complessi sono gruppi di Lie. Molti gruppi importanti in fisica e chimica sono gruppi di Lie e la loro teoria delle rappresentazioni è cruciale per l'applicazione della teoria dei gruppi in questi campi.

La teoria delle rappresentazioni è uno strumento utile in quanto riduce problemi di algebra astratta a problemi di algebra lineare. Inoltre lo spazio vettoriale su cui (per esempio) un gruppo è rappresentato può essere di dimensione infinita. Se questo, per esempio, è uno spazio di Hilbert, allora i metodi dell'analisi funzionale possono essere applicati alla teoria dei gruppi.^[3][4] La teoria delle rappresentazioni è importante anche in fisica poiché, per esempio, descrive come il gruppo di simmetria di un sistema fisico influenza le soluzioni delle equazioni che descrivono il sistema.^[5]

La teoria delle rappresentazioni è presente in tutti i campi della matematica per due ragioni. In primo luogo, le applicazioni della teoria delle rappresentazioni sono diverse; oltre al suo impatto sull'algebra, la teoria delle rappresentazioni:

• rende più chiara e generalizza l'analisi di Fourier tramite l'analisi armonica;
• è connessa alla geometria tramite la teoria degli invarianti e il programma di Erlangen;
• ha un impatto sulla teoria dei numeri tramite le forme automorfe e il programma Langlands.

In secondo luogo, ci sono diversi approcci alla teoria delle rappresentazioni. Gli stessi oggetti possono essere studiati usando metodi della geometria algebrica, della teoria dei moduli, della teoria analitica dei numeri, della geometria differenziale, della teoria degli operatori, della combinatoria algebrica e della topologia.

Il successo della teoria delle rappresentazioni ha portato a numerose generalizzazioni. Una delle versioni più generali si ha nella teoria delle categorie. Gli oggetti algebrici a cui si applica la teoria delle rappresentazioni possono essere visti come particolari tipi di categorie e le rappresentazioni come funtori dalla categoria degli oggetti algebrici considerati alla categoria degli spazi vettoriali.^[6] Questa descrizione indica due ovvie generalizzazioni: primo, gli oggetti algebrici possono essere sostituiti da categorie più generali; secondo, la categoria di arrivo degli spazi vettoriali può essere sostituita da altre categorie ben studiate.

Sia ${\displaystyle V}$ uno spazio vettoriale su un campo ${\displaystyle F}$. Per esempio supponiamo che ${\displaystyle V}$ sia ${\displaystyle \mathbb {R} ^{n}}$ o ${\displaystyle \mathbb {C} ^{n},}$ lo spazio vettoriale ${\displaystyle n}$-dimensionale standard sui reali o sui complessi, rispettivamente. In questo caso, l'idea della teoria delle rappresentazioni è lavorare con l'algebra astratta in concreto usando le matrici ${\displaystyle n\times n}$ di numeri reali o complessi.

Ci sono tre tipi principali di oggetti algebrici su cui può essere fatto: gruppi, algebre associative e algebre di Lie.^[6]

• L'insieme di tutte le matrici invertibili di ordine ${\displaystyle n}$ è un gruppo rispetto alla moltiplicazione di matrici e la teoria delle rappresentazioni dei gruppi analizza un gruppo descrivendo ("rappresentando") i suoi elementi in termini di matrici invertibili.
• L'addizione e la moltiplicazione di matrici rendono l'insieme di tutte le matrici ${\displaystyle n\times n}$ un'algebra associativa, e quindi esiste una corrispondente teoria delle rappresentazioni delle algebre associative.
• Se sostituiamo la moltiplicazione di matrici ${\displaystyle MN}$ con il commutatore di matrici ${\displaystyle MN-NM,}$ l'insieme delle matrici di ordine ${\displaystyle n}$ diventa invece un'algebra di Lie, portando a una teoria delle rappresentazioni delle algebre di Lie.

Questo si generalizza a qualsiasi campo ${\displaystyle F}$ e qualsiasi spazio vettoriale ${\displaystyle V}$ su ${\displaystyle F,}$ sostituendo le matrici con le funzioni lineari e la moltiplicazione di matrici con la composizione; cioè, per ogni spazio vettoriale ${\displaystyle V}$ su ${\displaystyle F}$ esiste un gruppo GL(V,F) di automorfismi di ${\displaystyle V,}$ essite un'algebra associativa ${\displaystyle \mathrm {End} _{F}(V)}$ di tutti endomorfismi di ${\displaystyle V,}$ e una corrispondente algebra di Lie ${\displaystyle {\mathfrak {gl}}(V,F).}$

Ci sono due modi per definire una rappresentazione. Il primo utilizza l'idea di azione di gruppo, generalizzando il modo in cui le matrici agiscono sui vettori colonna mediante la moltiplicazione matriciale. Una rappresentazione di un gruppo ${\displaystyle G}$ o di un'algebra (associativa o di Lie) ${\displaystyle A}$ su uno spazio vettoriale ${\displaystyle V}$ è una funzione

${\displaystyle \Phi \colon G\times V\to V,\quad {\text{oppure}}\quad \Phi \colon A\times V\to V,}$

con due proprietà. Primo, per ogni ${\displaystyle g\in G}$ (o ${\displaystyle a\in A}$), la funzione

${\displaystyle {\begin{aligned}\Phi (g)\colon V&\to V\\v&\mapsto \Phi (g,v)\end{aligned}}}$

è lineare (su ${\displaystyle F}$). Secondo, se introduciamo la notazione ${\displaystyle g\cdot v}$ per ${\displaystyle \Phi (g,v),}$ per ogni ${\displaystyle g_{1},g_{2}\in G}$ e ${\displaystyle v\in V}$:

${\displaystyle (1)\quad e\cdot v=v,}$

${\displaystyle (2)\quad g_{1}\cdot (g_{2}\cdot v)=(g_{1}g_{2})\cdot v,}$

dove ${\displaystyle e}$ è l'elemento neutro di ${\displaystyle G}$ e ${\displaystyle g_{1}g_{2}}$ è il prodotto in ${\displaystyle G.}$ Il requisito per le algebre associative è analogo, tranne per il fatto che le algebre associative non hanno sempre un elemento neutro, nel qual caso l'equazione (1) viene ignorata. L'equazione (2) è un'espressione astratta dell'associatività della moltiplicazione di matrici. Questo non vale per il commutatore di matrici e inoltre non vi è alcun elemento neutro per il commutatore. Quindi per le algebre di Lie, l'unico requisito è che per ogni ${\displaystyle x_{1},x_{2}\in A}$ e ${\displaystyle v\in V}$:

${\displaystyle (2')\quad x_{1}\cdot (x_{2}\cdot v)-x_{2}\cdot (x_{1}\cdot v)=[x_{1},x_{2}]\cdot v,}$

dove ${\displaystyle [x_{1},x_{2}]}$ è la parentesi di Lie, che generalizza il commutatore di matrici ${\displaystyle MN-NM.}$

Il secondo modo per definire una rappresentazione è tramite la funzione ${\displaystyle \varphi }$ che manda ${\displaystyle g\in G}$ in una funzione lineare ${\displaystyle \varphi (g)\colon V\to V,}$ che soddisfa

${\displaystyle \varphi (g_{1}g_{2})=\varphi (g_{1})\circ \varphi (g_{2}),\quad {\text{per ogni }}g_{1},g_{2}\in G,}$

e analogamente negli altri casi. Questo approccio è più conciso e più astratto. Da questo punto di vista:

• una rappresentazione di un gruppo ${\displaystyle G}$ su uno spazio vettoriale ${\displaystyle V}$ è un omomorfismo di gruppi ${\displaystyle \varphi \colon G\to \mathrm {GL} (V,F)}$;^[7]
• una rappresentazione di un'algebra associativa ${\displaystyle A}$ su uno spazio vettoriale ${\displaystyle V}$ è un omomorfismo di algebre ${\displaystyle \varphi \colon A\to \mathrm {End} _{F}(V)}$;
• una rappresentazione di un'algebra di Lie ${\displaystyle {\mathfrak {a}}}$ su uno spazio vettoriale ${\displaystyle V}$ è un omomorfismo di algebre di Lie ${\displaystyle \varphi \colon {\mathfrak {a}}\to {\mathfrak {gl}}(V,F)}$.

Lo spazio vettoriale ${\displaystyle V}$ è chiamato spazio di rappresentazione di ${\displaystyle \varphi }$ e la sua dimensione (se finita) è chiamata dimensione della rappresentazione (a volte grado, come in ^[8]). È anche pratica comune riferirsi a ${\displaystyle V}$ stesso come alla rappresentazione quando l'omomorfismo ${\displaystyle \varphi }$ è chiaro dal contesto; altrimenti la notazione ${\displaystyle (V,\varphi )}$ può essere usata per indicare una rappresentazione.

Quando ${\displaystyle V}$ è di dimensione finita ${\displaystyle n,}$ si può scegliere una base per ${\displaystyle V}$ per identificare ${\displaystyle V}$ con ${\displaystyle F^{n},}$ e quindi recuperare una rappresentazione matriciale con elementi nel campo ${\displaystyle F.}$

Una rappresentazione effettiva o fedele è una rappresentazione ${\displaystyle (V,\varphi ),}$ per la quale l'omomorfismo ${\displaystyle \varphi }$ è iniettivo.

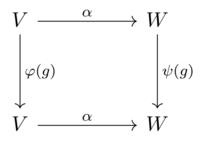
Se ${\displaystyle V}$ e ${\displaystyle W}$ sono spazi vettoriali su ${\displaystyle F,}$ con rappresentazioni ${\displaystyle \varphi }$ e ${\displaystyle \psi }$ di un gruppo ${\displaystyle G,}$ allora una funzione equivariante da ${\displaystyle V}$ a ${\displaystyle W}$ è una funzione lineare ${\displaystyle \alpha \colon V\to W}$ tale che

${\displaystyle \alpha (g\cdot v)=g\cdot \alpha (v),}$

per ogni ${\displaystyle g\in G}$ e ${\displaystyle v\in V.}$ In termini di ${\displaystyle \varphi \colon G\to \mathrm {GL} (V)}$ e ${\displaystyle \psi \colon G\to \mathrm {GL} (W),}$ questo significa

${\displaystyle \alpha \circ \varphi (g)=\psi (g)\circ \alpha ,}$

per ogni ${\displaystyle g\in G,}$ cioè, il diagramma seguente commuta:

Le funzioni equivarianti per le rappresentazioni di un'algebra associativa o di Lie sono definite in modo simile. Se ${\displaystyle \alpha }$ è invertibile, allora si dice che è un isomorfismo, nel qual caso ${\displaystyle V}$ e ${\displaystyle W}$ (o, più precisamente, ${\displaystyle \varphi }$ e ${\displaystyle \psi }$) sono rappresentazioni isomorfe, anche dette rappresentazioni equivalenti. Una funzione equivariante è spesso chiamata funzione intrecciata delle rappresentazioni. Inoltre, nel caso di un gruppo ${\displaystyle G,}$ a volte è chiamato ${\displaystyle G}$-funzione.

Le rappresentazioni isomorfe sono, per scopi pratici, "le stesse"; forniscono le stesse informazioni sul gruppo o sull'algebra rappresentati. La teoria delle rappresentazioni cerca quindi di classificare le rappresentazioni a meno di isomorfismo.

Se ${\displaystyle (V,\psi )}$ è una rappresentazione di un gruppo ${\displaystyle G,}$ e ${\displaystyle W}$ è un sottospazio vettoriale di ${\displaystyle V}$ che è preservato dall'azione di ${\displaystyle G,}$ ossia per ogni ${\displaystyle w\in W}$ e ${\displaystyle g\in G,}$ si ha ${\displaystyle g\cdot w\in W}$ (Serre chiama ${\displaystyle W}$ stabile rispetto a ${\displaystyle G}$), quindi ${\displaystyle W}$ è chiamata sottorappresentazione. Definendo

${\displaystyle \phi \colon G\to {\text{Aut}}(W),}$

dove ${\displaystyle \phi (g)}$ è la restrizione di ${\displaystyle \psi (g)}$ per ${\displaystyle W,}$ allora ${\displaystyle (W,\phi )}$ è una rappresentazione di ${\displaystyle G}$ e l'inclusione di ${\displaystyle W\hookrightarrow V}$ è una funzione equivariante. Anche lo spazio quoziente ${\displaystyle V/W}$ ha una struttura di rappresentazione di ${\displaystyle G}$. Se ${\displaystyle V}$ ha esattamente due sottorappresentazioni, vale a dire il sottospazio banale ${\displaystyle \{0\}}$ e ${\displaystyle V}$ stessa, allora la rappresentazione è detta irriducibile. Se ${\displaystyle V}$ ha una sottorappresentazione non banale propria, si dice che la rappresentazione è riducibile.^[9] La definizione di rappresentazione irriducibile implica il lemma di Schur: una funzione equivariante

${\displaystyle \alpha :(V,\psi )\to (V',\psi ')}$

tra rappresentazioni irriducibili o è la funzione zero o è un isomorfismo, poiché il nucleo e l'immagine sono sottorappresentazioni. In particolare, quando ${\displaystyle V=V',}$ questo mostra che gli endomorfismi equivarianti di ${\displaystyle V}$ formano un'algebra di divisione associativa sul campo sottostante ${\displaystyle F.}$ Se ${\displaystyle F}$ è algebricamente chiuso, gli unici endomorfismi equivarianti di una rappresentazione irriducibile sono i multipli scalari dell'identità. Le rappresentazioni irriducibili sono gli elementi costitutivi della teoria delle rappresentazioni per molti gruppi: se una rappresentazione ${\displaystyle V}$ non è irriducibile, allora è costruita apartire da una sottorappresentazione e da un quoziente entrambi, in un certo senso, "più semplici". Per esempio, se ${\displaystyle V}$ è di dimensione finita, allora sia la sottorappresentazione che il quoziente hanno dimensione minore. Ci sono controesempi in cui una rappresentazione ha una sottorappresentazione, ma ha solo una componente irriducibile non banale. Ad esempio, il gruppo additivo ${\displaystyle (\mathbb {R} ,+)}$ ha una rappresentazione bidimensionale

${\displaystyle \phi (a)={\begin{bmatrix}1&a\\0&1\end{bmatrix}}.}$

Questo gruppo ha il vettore ${\displaystyle {\begin{bmatrix}1\\0\end{bmatrix}}}$ fissato da questo omomorfismo, ma il sottospazio complementare manda

${\displaystyle {\begin{bmatrix}0\\1\end{bmatrix}}\mapsto {\begin{bmatrix}a\\1\end{bmatrix}}}$

dando solo una sottorappresentazione irriducibile. Questo è vero per tutti i gruppi unipotenti^{[10], pag. 112}.

Se ${\displaystyle (V,\varphi )}$ e ${\displaystyle (W,\psi )}$ sono rappresentazioni di un gruppo ${\displaystyle G,}$ allora la somma diretta di ${\displaystyle V}$ e ${\displaystyle W}$ è una rappresentazione, in modo canonico, tramite l'identificazione

${\displaystyle g\cdot (v,w)=(g\cdot v,g\cdot w).}$

La somma diretta di due rappresentazioni non dà maggiori informazioni sul gruppo ${\displaystyle G}$ rispetto a quelle che le due rappresentazioni danno individualmente. Se una rappresentazione è la somma diretta di due sottorappresentazioni proprie non banali, si dice decomponibile. Altrimenti, si dice indecomponibile.

In circostanze favorevoli, ogni rappresentazione di dimensione finita è una somma diretta di rappresentazioni irriducibili: tali rappresentazioni si dicono semisemplici. In questo caso, è sufficiente studiare solo le rappresentazioni irriducibili. Esempi in cui si verifica questo fenomeno di "riducibilità completa" includono i gruppi finiti (vedere il teorema di Maschke), i gruppi compatti e le algebre di Lie semisemplici.

Nei casi in cui la riducibilità completa non vale, si deve capire come le rappresentazioni indecomponibili possono essere costruite da rappresentazioni irriducibili come estensioni di un quoziente con una sottorappresentazione.

Supponiamo che ${\displaystyle \phi _{1}\colon G\rightarrow \mathrm {GL} (V_{1})}$ e ${\displaystyle \phi _{2}\colon G\rightarrow \mathrm {GL} (V_{2})}$ siano rappresentazioni di un gruppo ${\displaystyle G.}$ Allora possiamo formare una rappresentazione ${\displaystyle \phi _{1}\otimes \phi _{2}}$ di ${\displaystyle G}$ che agisce sullo spazio vettoriale del prodotto tensoriale ${\displaystyle V_{1}\otimes V_{2}}$ nel seguente modo:

${\displaystyle (\phi _{1}\otimes \phi _{2})(g)=\phi _{1}(g)\otimes \phi _{2}(g).}$

Se ${\displaystyle \phi _{1}}$ e ${\displaystyle \phi _{2}}$ sono rappresentazioni di un'algebra di Lie, la formula corretta da usare è

${\displaystyle (\phi _{1}\otimes \phi _{2})(X)=\phi _{1}(X)\otimes I+I\otimes \phi _{2}(X).}$

Questo prodotto può essere riconosciuto come un coprodotto su una coalgebra. In generale, il prodotto tensoriale di rappresentazioni irriducibili non è irriducibile. Il processo di decomposizione di un prodotto tensoriale come somma diretta di rappresentazioni irriducibili è noto come teoria di Clebsch-Gordan.

Nel caso della teoria delle rappresentazioni del gruppo ${\displaystyle \mathrm {SU} (2)}$ (o equivalentemente, della sua algebra di Lie complessificata ${\displaystyle {\mathfrak {sl}}(2;\mathbb {C} )}$), la decomposizione è facile da determinare. Le rappresentazioni irriducibili sono parametrizzate da un parametro ${\displaystyle l}$ che è un numero intero non negativo o un numero semintero; la rappresentazione ha quindi dimensione ${\displaystyle 2l+1}$. Supponiamo di prendere la rappresentazione prodotto tensoriale di due rappresentazioni, associate a ${\displaystyle l_{1}}$ e ${\displaystyle l_{2},}$ dove assumiamo ${\displaystyle l_{1}\geq l_{2}}$. Allora il prodotto tensoriale si decompone come somma diretta di una copia di ciascuna rappresentazione associata a ${\displaystyle l,}$ dove ${\displaystyle l}$ va da ${\displaystyle l_{1}-l_{2}}$ a ${\displaystyle l_{1}+l_{2}}$ con incrementi di 1. Se, ad esempio, ${\displaystyle l_{1}=l_{2}=1}$, i valori di ${\displaystyle l}$ che si considerano sono 0, 1 e 2. Quindi, la rappresentazione prodotto tensoriale di dimensione ${\displaystyle 3\times 3=9}$ si decompone come somma diretta di una rappresentazione unidimensionale ${\displaystyle (l=0),}$ una rappresentazione tridimensionale ${\displaystyle (l=1),}$ e una rappresentazione a 5 dimensioni ${\displaystyle (l=2)}$.

La teoria delle rappresentazioni ha un notevole numero di branche e di approcci allo studio delle rappresentazioni di gruppi e algebre. Sebbene tutte le teorie abbiano in comune i concetti di base già discussi, differiscono notevolmente nei dettagli. Le differenze sono almeno tre:

1. La teoria delle rappresentazioni dipende dal tipo di oggetto algebrico rappresentato. Esistono diverse classi di gruppi, algebre associative e algebre di Lie, e le loro teorie delle rappresentazioni hanno ciascuna una sua caratterizzazione.
2. La teoria delle rappresentazioni dipende dalla natura dello spazio vettoriale su cui è rappresentato l'oggetto algebrico. La distinzione più importante è tra rappresentazioni a dimensione finita e rappresentazioni a dimensione infinita. Nel caso di dimensione infinita, le strutture aggiuntive sono particolarmente importanti (ad esempio, se lo spazio è uno spazio di Hilbert, uno spazio di Banach, ecc.). Strutture algebriche aggiuntive possono essere considerate anche nel caso di dimensione finita.
3. La teoria delle rappresentazioni dipende dal tipo di campo su cui è definito lo spazio vettoriale. I casi più importanti sono il campo dei numeri complessi, il campo dei numeri reali, i campi finiti e i campi dei numeri p-adici. Ulteriori difficoltà sorgono per i campi di caratteristica positiva e per i campi che non sono chiusi algebricamente.

Le rappresentazioni dei gruppi sono uno strumento molto importante nello studio dei gruppi finiti. Sorgono anche nelle applicazioni della teoria dei gruppi finiti alla geometria e alla cristallografia. Le rappresentazioni di gruppi finiti mostrano molte delle caratteristiche della teoria generale e suggeriscono gli approcci da adottare ad altre branche della teoria delle rappresentazioni.

Su un campo di caratteristica zero, la rappresentazione di un gruppo finito ${\displaystyle G}$ ha molte proprietà utili. In primo luogo, le rappresentazioni di ${\displaystyle G}$ sono semisemplici (ossia completamente riducibili). Questa è una conseguenza del teorema di Maschke, che afferma che qualsiasi sottorappresentazione ${\displaystyle V}$ di una ${\displaystyle G}$-rappresentazione ${\displaystyle W}$ ha un complemento ${\displaystyle G}$-invariante. Una dimostrazione si ha scegliendo una qualsiasi proiezione ${\displaystyle \pi }$ da ${\displaystyle W}$ a ${\displaystyle V}$ e sostituirla con la sua media ${\displaystyle \pi _{G}}$ definita da

${\displaystyle \pi _{G}(x)={\frac {1}{|G|}}\sum _{g\in G}g\cdot \pi (g^{-1}\cdot x).}$

La funzione ${\displaystyle \pi _{G}}$ è equivariante e il suo nucleo è il complemento richiesto.

Le rappresentazioni finito-dimensionali di ${\displaystyle G}$ possono essere ben studiate e comprese usando la teoria dei caratteri: il carattere di una rappresentazione ${\displaystyle \varphi \colon G\to \mathrm {GL} (V)}$ è la funzione di classe ${\displaystyle \chi _{\varphi }\colon G\to F}$ definita da

${\displaystyle \chi _{\varphi }(g)=\mathrm {Tr} (\varphi (g)),}$

dove ${\displaystyle \mathrm {Tr} }$ è la traccia. Una proprietà fondamentali della teoria dei caratteri per gruppi finiti è che una rappresentazione irriducibile di ${\displaystyle G}$ è completamente determinata dal suo carattere.

Il teorema di Maschke vale più in generale per i campi di caratteristica positiva ${\displaystyle p,}$ come i campi finiti, purché il primo ${\displaystyle p}$ sia coprimo con l'ordine di ${\displaystyle G.}$ Quando ${\displaystyle p}$ divide ${\displaystyle |G|,}$ ci sono rappresentazioni di ${\displaystyle G}$ che non sono semisemplici e che vengono studiate in una sottobranca chiamata teoria delle rappresentazioni modulari.

Le tecniche di calcolo della media mostrano anche che se ${\displaystyle F}$ è il campo reale o complesso, qualsiasi rappresentazione di ${\displaystyle G}$ preserva un prodotto scalare ${\displaystyle \langle \cdot ,\cdot \rangle }$ su ${\displaystyle V}$ nel senso che

${\displaystyle \langle g\cdot v,g\cdot w\rangle =\langle v,w\rangle ,}$

per ogni ${\displaystyle g\in G}$ e ${\displaystyle v,w\in W.}$ Quindi ogni rappresentazione di ${\displaystyle G}$ è unitaria.

Le rappresentazioni unitarie sono automaticamente semisemplici, poiché il risultato di Maschke può essere dimostrato prendendo il complemento ortogonale di una sottorappresentazione. Quando si studiano rappresentazioni di gruppi che non sono finiti, le rappresentazioni unitarie forniscono una buona generalizzazione delle rappresentazioni reali e complesse di un gruppo finito.

Risultati come il teorema di Maschke e la proprietà di essere unitaria, che si basano sulla media, possono essere generalizzati a gruppi più generali sostituendo la media discreta con un integrale, a condizione che sia possibile definire una nozione adeguata di integrale. Questo può essere fatto per gruppi topologici compatti (compresi i gruppi di Lie compatti), utilizzando la misura di Haar, e la teoria risultante è nota come analisi armonica astratta.

Su campi arbitrari, un'altra classe di gruppi finiti che hanno una buona teoria delle rappresentazioni sono i gruppi finiti di tipo Lie. Esempi importanti sono i gruppi algebrici lineari su campi finiti. La teoria delle rappresentazioni dei gruppi algebrici lineari e dei gruppi di Lie estende questi esempi a gruppi a dimensione infinita. Questi ultimi sono strettamente collegati alle rappresentazioni delle algebre di Lie. L'importanza della teoria dei caratteri per i gruppi finiti ha un analogo nella teoria dei pesi per le rappresentazioni dei gruppi di Lie e delle algebre di Lie.

Le rappresentazioni di un gruppo finito ${\displaystyle G}$ sono anche collegate direttamente alle rappresentazioni di algebre tramite l'algebra di gruppo ${\displaystyle F[G],}$ che è uno spazio vettoriale su ${\displaystyle F}$ con gli elementi di ${\displaystyle G}$ come base, dotato dell'operazione di moltiplicazione definita dall'operazione di gruppo, di linearità e del requisito che le operazioni di gruppo e la moltiplicazione per uno scalare commutino.

Le rappresentazioni modulari di un gruppo finito ${\displaystyle G}$ sono rappresentazioni su un campo la cui caratteristica non è coprima con ${\displaystyle |G|,}$ quindi il teorema di Maschke non vale più (perché ${\displaystyle |G|}$ non è invertibile in ${\displaystyle F}$ e quindi non si può dividere per esso). Tuttavia, Richard Brauer estese gran parte della teoria dei caratteri alle rappresentazioni modulari, e questa teoria giocò un ruolo importante nei primi progressi verso la classificazione dei gruppi semplici finiti, specialmente per i gruppi semplici la cui caratterizzazione non era ottenibile con metodi puri di teoria dei gruppi perché i loro sottogruppi 2-Sylow erano "troppo piccoli".

Oltre ad avere applicazioni alla teoria dei gruppi, le rappresentazioni modulari sorgono naturalmente in altri rami della matematica, come la geometria algebrica, la teoria dei codici, la combinatoria e la teoria dei numeri.

Una rappresentazione unitaria di un gruppo ${\displaystyle G}$ è una rappresentazione lineare ${\displaystyle \varphi }$ di ${\displaystyle G}$ su uno spazio di Hilbert reale o (solitamente) complesso ${\displaystyle V}$ tale che ${\displaystyle \varphi (g)}$ è un operatore unitario per ogni ${\displaystyle g\in G.}$ Tali rappresentazioni sono state ampiamente applicate nella meccanica quantistica sin dagli anni '20, grazie, in particolare, all'influenza di Hermann Weyl, e questo ha ispirato lo sviluppo della teoria, in particolare attraverso l'analisi delle rappresentazioni del gruppo di Poincaré di Eugene Wigner. Uno dei pionieri nella costruzione di una teoria generale delle rappresentazioni unitarie (per qualsiasi gruppo ${\displaystyle G}$ piuttosto che solo per gruppi particolari utili nelle applicazioni) è stato George Mackey, e una teoria estesa è stata sviluppata da Harish-Chandra e altri negli anni '50 e '60.

Uno degli obiettivi principali è descrivere il "duale unitario", lo spazio delle rappresentazioni unitarie irriducibili di ${\displaystyle G.}$ La teoria è più sviluppata nel caso in cui ${\displaystyle G}$ sia un gruppo topologico localmente compatto (di Hausdorff) e le rappresentazioni sono fortemente continue. Per ${\displaystyle G}$ abeliano, il duale unitario è solo lo spazio dei caratteri, mentre per ${\displaystyle G}$ compatto, il teorema di Peter-Weyl mostra che le rappresentazioni unitarie irriducibili sono di dimensione finita e il duale unitario è discreto. Ad esempio, se ${\displaystyle G}$ è il gruppo ${\displaystyle S^{1},}$ i caratteri sono dati da numeri interi e il duale unitario è ${\displaystyle \mathbb {Z} .}$

Per ${\displaystyle G}$ non compatto, la questione di quali rappresentazioni siano unitarie è sottile. Sebbene le rappresentazioni unitarie irriducibili debbano essere "ammissibili" (come i moduli di Harish-Chandra) ed è facile determinare quali rappresentazioni ammissibili hanno una forma sesquilineare invariante non degenere, è difficile determinare quando questa forma è definita positiva. Una descrizione efficace del duale unitario, anche per gruppi che si comportano relativamente bene come i gruppi di Lie riduttivi reali (discussi di seguito), rimane un importante problema aperto nella teoria delle rappresentazioni. È stato risolto per molti gruppi particolari, come ${\displaystyle \mathrm {SL} (2,\mathbb {R} )}$ e il gruppo Lorentz.

La dualità tra il gruppo ${\displaystyle S^{1}}$ e il gruppo degli interi ${\displaystyle \mathbb {Z} ,}$ o più in generale, tra un toro ${\displaystyle T^{n}}$ e ${\displaystyle \mathbb {Z} ^{n}}$ è ben nota in analisi come teoria delle serie di Fourier, e la trasformata di Fourier esprime il fatto che lo spazio dei caratteri su uno spazio vettoriale reale è lo spazio vettoriale duale. Così la teoria della rappresentazioni unitarie e l'analisi armonica sono strettametne correlate, e l'analisi armonica astratta sfrutta questa relazione, sviluppando l'analisi di funzioni su gruppi topologici localmente compatti e spazi correlati.

Uno degli obiettivi principali è fornire una forma generale della trasformata di Fourier e del teorema di Plancherel. Ciò si ottiene costruendo una misura sul duale unitario e un isomorfismo tra la rappresentazione regolare di ${\displaystyle G}$ sullo spazio ${\displaystyle L^{2}(G)}$ di funzioni a quadrato integrabile su ${\displaystyle G}$ e la sua rappresentazione sullo spazio delle funzioni ${\displaystyle L^{2}}$ sul duale unitario. La dualità di Pontryagin e il teorema di Peter-Weyl raggiungono questo obiettivo rispettivamente per ${\displaystyle G}$ abeliano e per ${\displaystyle G}$ compatto.

Un altro approccio consiste nel considerare tutte le rappresentazioni unitarie, non solo quelle irriducibili. Queste formano una categoria e la dualità Tannaka-Kerin fornisce un modo per recuperare un gruppo compatto dalla sua categoria di rappresentazioni unitarie.

Se il gruppo non è né abeliano né compatto, nessuna teoria generale è nota e non c'è un analogo del teorema di Plancherel o di inversione di Fourier, sebbene Alexander Grothendieck abbia esteso la dualità di Tannaka-Kerin a una relazione tra gruppi algebrici lineari e categorie tannakiane.

L'analisi armonica è stata estesa anche dall'analisi di funzioni su un gruppo ${\displaystyle G}$ a funzioni su spazi omogenei per ${\displaystyle G.}$ La teoria è particolarmente ben sviluppata per gli spazi simmetrici e fornisce una teoria delle forme automorfe (discussa di seguito).

Un gruppo di Lie è un gruppo che è anche una varietà differenziabile. Molti gruppi classici di matrici sui numeri reali o complessi sono gruppi di Lie. Molti dei gruppi importanti in fisica e chimica sono gruppi di Lie e la loro teoria delle rappresentazioni è cruciale per l'applicazione della teoria dei gruppi in quei campi.

La teoria delle rappresentazioni dei gruppi di Lie può essere sviluppata prima considerando i gruppi compatti, ai quali si applicano i risultati della teoria delle rappresentazioni compatte. Questa teoria può essere estesa a rappresentazioni di dimensione finita di gruppi di Lie semisemplici usando il trucco unitario di Weyl: ogni gruppo di Lie reale semisemplice ${\displaystyle G}$ ha una complessificazione, che è un gruppo di Lie complesso ${\displaystyle G^{c},}$ e questo gruppo di Lie complesso ha un sottogruppo compatto massimale ${\displaystyle K.}$ Le rappresentazioni di dimensione finita di ${\displaystyle G}$ sono in stretta corrispondenza con quelle di ${\displaystyle K.}$

Un gruppo di Lie generale è un prodotto semidiretto di un gruppo di Lie risolubile e di un gruppo di Lie semisemplice (la decomposizione di Levi). La classificazione delle rappresentazioni di gruppi di Lie risolubili è intrattabile in generale, ma spesso facile nei casi pratici. Le rappresentazioni di prodotti semidiretti possono quindi essere analizzate mediante risultati generali denominati teoria di Mackey, che è una generalizzazione dei metodi utilizzati nella classificazione di Wigner delle rappresentazioni del gruppo di Poincaré.

Un'algebra di Lie su un campo ${\displaystyle F}$ è uno spazio vettoriale su ${\displaystyle F}$ dotato di un'operazione bilineare antisimmetrica chiamata parentesi di Lie, che soddisfa l'identità di Jacobi. Le algebre di Lie sorgono in particolare come spazi tangenti dei gruppi di Lie all'elemento neutro, portando alla loro interpretazione come "simmetrie infinitesimali". Un approccio importante alla teoria delle rappresentazioni dei gruppi di Lie è studiare la corrispondente teoria delle rappresentazioni delle algebre di Lie, anche se le rappresentazioni delle algebre di Lie sono comunque di interesse indipendentemente dai gruppi di Lie.

Le algebre di Lie, come i gruppi di Lie, hanno una decomposizione di Levi in parti semisemplici e risolubili, con la teoria delle rappresentazioni delle algebre di Lie risolubili che è intrattabile in generale. Al contrario, le rappresentazioni finito-dimensionali delle algebre di Lie semisemplici sono completamente comprese, dopo il lavoro di Élie Cartan. Una rappresentazione di un'algebra di Lie semisemplice ${\displaystyle {\mathfrak {g}}}$ viene analizzata scegliendo una sottoalgebra di Cartan, che è essenzialmente una sottoalgebra massimale generica ${\displaystyle {\mathfrak {h}}}$ di ${\displaystyle {\mathfrak {g}}}$ su cui le parentesi di Lie sono nulle ("algebra abeliana"). La rappresentazione di ${\displaystyle {\mathfrak {g}}}$ può essere decomposta in spazi peso che sono autospazi per l'azione di ${\displaystyle {\mathfrak {h}}}$ e sono l'analogo infinitesimale dei caratteri. La struttura delle algebre di Lie semisemplici riduce quindi l'analisi delle rappresentazioni a un'analisi combinatoria facilmente comprensibile dei possibili pesi.

Esistono molte classi di algebre di Lie a dimensione infinita le cui rappresentazioni sono state studiate. Tra queste, una classe importante sono le algebre di Kac–Moody. Prendono il nome da Victor Kac e Robert Moody, che le scoprirono indipendentemente. Queste algebre formano una generalizzazione delle algebre di Lie semisemplici di dimensione finita e condividono molte delle loro proprietà combinatorie. Ciò significa che hanno una classe di rappresentazioni che possono essere comprese allo stesso modo delle rappresentazioni delle algebre di Lie semisemplici.

Le algebre di Lie affini sono un caso speciale di algebre di Kac–Moody, che hanno particolare importanza in matematica e fisica teorica, in particolare nella teoria di campo conforme e nella teoria dei modelli risolvibili esattamente. Kac ha scoperto un'elegante dimostrazione di certe identità combinatorie, le identità di Macdonald, che si basa sulla teoria delle rappresentazioni delle algebre affini di Kac-Moody.

Le superalgebre di Lie sono generalizzazioni delle algebre di Lie in cui lo spazio vettoriale sottostante ha una ${\displaystyle \mathbb {Z} _{2}}$-graduazione, e la proprietà di antisimmetria delle parentesi di Lie e l'identità di Jacobi sono modificate con segni opportuni. La loro teoria delle rappresentazioni è simile alla teoria delle rappresentazioni delle algebre di Lie.

I gruppi algebrici lineari (o più in generale, schemi gruppo affini) sono analoghi nella geometria algebrica dei gruppi di Lie, ma su campi più generali rispetto a ${\displaystyle \mathbb {R} }$ o ${\displaystyle \mathbb {C} .}$ In particolare, su campi finiti, danno origine a gruppi finiti di tipo Lie. Sebbene i gruppi algebrici lineari abbiano una classificazione molto simile a quella dei gruppi di Lie, la loro teoria delle rappresentazioni è piuttosto diversa (e molto meno compresa) e richiede tecniche diverse, poiché la topologia di Zariski è relativamente debole e le tecniche dell'analisi non sono disponibili.

La teoria degli invarianti studia le azioni sulle varietà algebriche dal punto di vista del loro effetto sulle funzioni, che formano le rappresentazioni del gruppo. Classicamente, la teoria affrontava la questione della descrizione esplicita di funzioni polinomiali che non cambiano, o sono invarianti, sotto le trasformazioni di un dato gruppo lineare. L'approccio moderno analizza la scomposizione di queste rappresentazioni in componenti irriducibili.

La teoria degli invarianti dei gruppi infiniti è indissolubilmente legata allo sviluppo dell'algebra lineare, in particolare, alle teorie delle forme quadratiche e dei determinanti. Un altro argomento con una forte influenza reciproca è la geometria proiettiva, in cui la teoria invariante può essere utilizzata per organizzare il soggetto, e durante gli anni '60 David Mumford ha dato nuova vita al soggetto sotto forma della sua teoria geometrica degli invarianti.

La teoria delle rappresentazioni di gruppi di Lie semisemplici ha le sue radici nella teoria degli invarianti e il forte legame fra teoria delle rappresentazioni e geometria algebrica ha molte similitudini con la geometria differenziale, a cominciare dal programma di Erlangen di Felix Klein e le connessioni di Élie Cartan, che pongono i gruppi e la simmetria al centro della geometria. Gli sviluppi moderni collegano la teoria delle rappresentazioni e la teoria degli invarianti ad aree diverse come l'olonomia, gli operatori differenziali e la teoria di più variabili complesse.

Le forme automorfe sono una generalizzazione delle forme modulari a funzioni analitiche più generali, eventualmente di più variabili complesse, con proprietà di trasformazione simili. La generalizzazione prevede la sostituzione del gruppo modulare ${\displaystyle \mathrm {PSL} _{2}(\mathbb {R} )}$ e del sottogruppo di congruenza scelto con un gruppo di Lie semisemplice ${\displaystyle G}$ e un sottogruppo discreto ${\displaystyle \Gamma .}$ Proprio come le forme modulari possono essere viste come forme differenziali su un quoziente del semipiano superiore complesso ${\displaystyle {\mathcal {H}}=\mathrm {PSL} _{2}(\mathbb {R} )/\mathrm {SO} (2),}$ le forme automorfe possono essere viste come forme differenziali (o oggetti simili) su ${\displaystyle \Gamma \backslash G/K,}$ dove ${\displaystyle K}$ è (tipicamente) un sottogruppo compatto massimale di ${\displaystyle G.}$ Tuttavia, è necessaria una certa attenzione, poiché il quoziente ha tipicamente delle singolarità. Il quoziente di un gruppo di Lie semisemplice per un sottogruppo compatto è uno spazio simmetrico e quindi la teoria delle forme automorfe è strettamente correlata all'analisi armonica su spazi simmetrici.

Prima dello sviluppo della teoria generale, molti casi speciali importanti sono stati elaborati in dettaglio, comprese le forme modulari di Hilbert e le forme modulari di Siegel. Risultati importanti nella teoria includono la formula della traccia di Selberg e la realizzazione da parte di Robert Langlands che il teorema di Riemann-Roch potrebbe essere applicato per calcolare la dimensione dello spazio delle forme automorfe. La successiva nozione di "rappresentazione automorfa" si è dimostrata di grande valore tecnico per trattare il caso in cui ${\displaystyle G}$ è un gruppo algebrico, trattato come un gruppo algebrico adelico. Di conseguenza, un'intera filosofia, il programma Langlands, si è sviluppata attorno alla relazione tra le rappresentazioni e le proprietà aritmetiche delle forme automorfe.

In un certo senso, le rappresentazioni di algebre associative generalizzano sia le rappresentazioni di gruppi che di algebre di Lie. Una rappresentazione di un gruppo induce una rappresentazione di un anello di gruppo o di un'algebra di gruppo corrispondente, mentre le rappresentazioni di un'algebra di Lie corrispondono biiettivamente alle rappresentazioni della sua algebra inviluppante universale. Tuttavia, la teoria delle rappresentazioni di generali algebre associative non ha tutte le belle proprietà della teoria delle rappresentazioni dei gruppi e delle algebre di Lie.

Quando si considerano le rappresentazioni di un'algebra associativa, si può dimenticare il campo sottostante e considerare semplicemente l'algebra associativa come un anello e le sue rappresentazioni come moduli. Questo approccio è sorprendentemente fruttuoso: molti risultati nella teoria delle rappresentazioni possono essere interpretati come casi speciali di risultati sui moduli su un anello.

Le algebre di Hopf forniscono un modo per migliorare la teoria delle rappresentazioni delle algebre associative, pur mantenendo la teoria delle rappresentazioni dei gruppi e delle algebre di Lie come casi speciali. In particolare, il prodotto tensoriale di due rappresentazioni è una rappresentazione, così come lo spazio vettoriale duale.

Le algebre di Hopf associate ai gruppi hanno una struttura algebrica commutativa, e quindi le algebre di Hopf generali sono conosciute come gruppi quantici, sebbene questo termine sia spesso limitato a certe algebre di Hopf che sorgono come deformazioni di gruppi o loro algebre inviluppanti universali. La teoria delle rappresentazioni dei gruppi quantici ha aggiunto sorprendenti intuizioni alla teoria delle rappresentazioni dei gruppi di Lie e delle algebre di Lie, ad esempio attraverso la base cristallina di Kashiwara.

Una rappresentazione di insieme (nota anche come azione di gruppo o rappresentazione di permutazione) di un gruppo ${\displaystyle G}$ su un insieme ${\displaystyle X}$ è data da una funzione ${\displaystyle \rho }$ da ${\displaystyle G}$ a ${\displaystyle X^{X},}$ l'insieme delle funzioni da ${\displaystyle X}$ a ${\displaystyle X,}$ tale che per ogni ${\displaystyle g_{1},g_{2}\in G}$ e per ogni ${\displaystyle x\in X}$:

${\displaystyle \rho (1)[x]=x;}$

${\displaystyle \rho (g_{1}g_{2})[x]=\rho (g_{1})[\rho (g_{2})[x]].}$

Queste condizioni e gli assiomi di un gruppo implicano che ${\displaystyle \rho (g)}$ è una biiezione (o permutazione) per ogni ${\displaystyle g\in G.}$ Quindi possiamo definire in modo equivalente una rappresentazione di permutazione come un omomorfismo di gruppi da ${\displaystyle G}$ al gruppo simmetrico ${\displaystyle S_{X}}$ di ${\displaystyle X.}$

Ogni gruppo ${\displaystyle G}$ può essere visto come una categoria con un unico oggetto; i morfismi in questa categoria sono solo gli elementi di ${\displaystyle G.}$ Data una categoria arbitraria ${\displaystyle C,}$ una rappresentazione di ${\displaystyle G}$ in ${\displaystyle C}$ è un funtore da ${\displaystyle G}$ a ${\displaystyle C.}$ Un tale funtore seleziona un oggetto ${\displaystyle X}$ in ${\displaystyle C}$ e un omomorfismo di gruppi da ${\displaystyle G}$ ad ${\displaystyle \mathrm {Aut} (X),}$ il gruppo degli automorfismi di ${\displaystyle X.}$

Nel caso in cui ${\displaystyle C}$ sia ${\displaystyle \mathbf {Vect} _{F},}$ la categoria degli spazi vettoriali su un campo ${\displaystyle F,}$ questa definizione è equivalente a una rappresentazione lineare. Allo stesso modo, una rappresentazione di insieme è solo una rappresentazione di ${\displaystyle G}$ nella categoria degli insiemi.

Per un altro esempio si consideri la categoria degli spazi topologici, Top. Le rappresentazioni in Top sono omomorfismi da ${\displaystyle G}$ al gruppo degli omeomorfismi di uno spazio topologico ${\displaystyle X.}$

Due tipi di rappresentazioni strettamente correlate alle rappresentazioni lineari sono:

• le rappresentazioni proiettive: nella categoria degli spazi proiettivi. Questi possono essere descritti come "rappresentazioni lineari a meno di trasformazioni scalari".
• le rappresentazioni affini: nella categoria degli spazi affini. Ad esempio, il gruppo euclideo agisce in modo affine sullo spazio euclideo.

Poiché i gruppi sono categorie, si possono anche considerare rappresentazioni di altre categorie. La generalizzazione più semplice è quella dei monoidi, che sono categorie con un oggetto. I gruppi sono monoidi per i quali ogni morfismo è invertibile. I monoidi generali hanno rappresentazioni in qualsiasi categoria. Nella categoria degli insiemi, queste sono azioni di monoidi, ma è possibile studiare rappresentazioni di monoidi su spazi vettoriali e altri oggetti.

Più in generale, si può allentare l'ipotesi che la categoria rappresentata abbia un solo oggetto. In generale, questa è semplicemente la teoria dei funtori tra categorie e si può dire poco.

Un caso speciale ha avuto un impatto significativo sulla teoria delle rappresentazioni, vale a dire la teoria delle rappresentazioni dei quiver. Un quiver è un grafo orientato (che consente cicli e frecce multiple), ma può essere trasformato in una categoria (e anche in un'algebra) considerando i cammini nel grafo. Le rappresentazioni di tali categorie/algebre hanno illuminato diversi aspetti della teoria delle rappresentazioni, ad esempio consentendo di ridurre in alcuni casi domande di teoria delle rappresentazioni non semisemplici a un gruppo a domande di teoria delle rappresentazioni semisemplici su un quiver.

• J. L. Alperin, Local Representation Theory: Modular Representations as an Introduction to the Local Representation Theory of Finite Groups, 1986, ISBN 978-0-521-44926-7.
• Armand Borel, Essays in the History of Lie Groups and Algebraic Groups, 2001, ISBN 978-0-8218-0288-5.
• 1962, ISBN 978-0-470-18975-7, https://archive.org/details/representationth11curt. Parametro titolo vuoto o mancante (aiuto)
• Stephen Gelbart, An Elementary Introduction to the Langlands Program, vol. 10, 1984, DOI:10.1090/S0273-0979-1984-15237-6.
• Brian Hall, Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Graduate Texts in Mathematics, vol. 222, 2nd, 2015, ISBN 978-3319134666.
• James E. Humphreys, Introduction to Lie Algebras and Representation Theory, 1972a, ISBN 978-0-387-90053-7.
• James E. Humphreys, Linear Algebraic Groups, Graduate Texts in Mathematics, vol. 21, 1972b, ISBN 978-0-387-90108-4.
• Victor Kac, Lie superalgebras, vol. 26, 1977, DOI:10.1016/0001-8708(77)90017-2.
• Victor Kac, Infinite Dimensional Lie Algebras, 3rd, 1990, ISBN 978-0-521-46693-6.
• Anthony Knapp, Representation Theory of Semisimple Groups: An Overview Based on Examples, 2001, ISBN 978-0-691-09089-4.
• Alexei Kostrikin e Yuri Manin, Linear Algebra and Geometry, 1997, ISBN 978-90-5699-049-7.
• Yurii I. Lyubich. Introduction to the Theory of Banach Representations of Groups. Translated from the 1985 Russian-language edition (Kharkov, Ukraine). Birkhäuser Verlag. 1988.
• David Mumford, J. Fogarty e F. Kirwan, Geometric invariant theory, Ergebnisse der Mathematik und ihrer Grenzgebiete (2) [Results in Mathematics and Related Areas (2)], vol. 34, 3rd, 1994, ISBN 978-3-540-56963-3, MR 0214602.; MR 0719371 (2nd ed.); MR 1304906(3rd ed.)
• Peter J. Olver, Classical invariant theory, 1999, ISBN 978-0-521-55821-1.
• Copia archiviata, vol. 97, 1927, DOI:10.1007/BF01447892. URL consultato il 26 settembre 2021 (archiviato dall'url originale il 19 agosto 2014).
• Lev Pontrjagin, The theory of topological commutative groups, vol. 35, 1934, DOI:10.2307/1968438, JSTOR 1968438.
• Jean-Pierre Serre, Linear Representations of Finite Groups, 1977, ISBN 978-0387901909.
• Shlomo Sternberg, Group Theory and Physics, 1994, ISBN 978-0-521-55885-3.
• Wu-Ki Tung, Group Theory in Physics, 1stª ed., New Jersey·London·Singapore·Hong Kong, World Scientific, 1985, ISBN 978-9971966577.
• Hermann Weyl, Gruppentheorie und Quantenmechanik, The Theory of Groups and Quantum Mechanics, translated H.P. Robertson, 1931, 1928, ISBN 978-0-486-60269-1.
• Hermann Weyl, The Classical Groups: Their Invariants and Representations, 2nd, 1946, ISBN 978-0-691-05756-9.
• Eugene Wigner, On unitary representations of the inhomogeneous Lorentz group, vol. 40, 1939, DOI:10.2307/1968551, JSTOR 1968551.

• Rappresentazione dei gruppi
• Rappresentazioni dei gruppi di Lie

• Wikimedia Commons contiene immagini o altri file su teoria delle rappresentazioni

• (EN) Representation theory, in Encyclopaedia of Mathematics, Springer e European Mathematical Society, 2002.
• Alexander Kirillov Jr., Un'introduzione ai gruppi di Lie e alle algebre di Lie (2008). Libro di testo, versione preliminare pdf scaricabile dalla home page dell'autore.
• Kevin Hartnett, (2020), articolo sulla teoria della rappresentazione nella rivista Quanta.

Controllo di autorità	GND (DE) 4148816-7 · NDL (EN, JA) 00563848