Théorème de Descartes (géométrie)

En géométrie, le théorème de Descartes, découvert par René Descartes, établit une relation entre quatre cercles tangents entre eux. Il peut être utilisé pour construire les cercles tangents à trois cercles donnés tangents deux à deux.

Histoire

Les problèmes géométriques concernant des cercles tangents sont très anciens. En Grèce antique, trois siècles avant Jésus-Christ, Apollonius de Perga a consacré un livre entier à ce sujet ; malheureusement ce livre, Les Contacts, a disparu. La construction d'un cercle tangent à trois cercles donnés (le plus difficile des problèmes qui figurait dans ce livre) est souvent appelé Problème d'Apollonius. Regiomontanus en a donné une solution algébrique au XV^e siècle mais ne croyait pas possible l'existence d'une solution géométrique, François Viète en a proposé la restauration à Adrien Romain, qui en a donné une solution bâtie sur des intersections d'hyperboles. Cette joute est l'occasion pour Viète de montrer la supériorité de son algèbre nouvelle par la publication de Apollonius Gallus^[1]. La grande finesse de Viète s'y montre à plein et Michel Chasles découvrira dans cet ouvrage les prémices de l'inversion plane.

René Descartes parle brièvement du problème en 1643, en considérant contrairement à ces prédécesseurs le cas de cercles mutuellement tangents, dans une lettre adressée à la princesse Élisabeth de Bohême à qui il avait soumis le problème^[2],[3]. Il a fourni essentiellement la même solution que celle donnée dans la formule ci-dessous, c'est pourquoi son nom a été donné au théorème.

Philip Beecroft, un mathématicien amateur, découvre en 1842 que les configurations de quatre cercles mutuellement tangents apparaissent en paires duales ayant les mêmes points de contact et en déduit une démonstration de la relation de Descartes^[4].

Émile Lemoine donne une solution géométrique du problème, minimale dans son système de mesure des constructions.

Frederick Soddy redécouvre la formule en 1936, d'où le nom de formule de Soddy-Descartes donné parfois à cette formule^[5]. Les cercles solutions de l'équation sont appelés cercles de Soddy. Ils sont parfois connus sous le nom de kissing circles, peut-être parce que Soddy a choisi d'éditer sa version du théorème sous forme de poésie intitulée The Kiss precise, qui a été imprimé dans Nature le 20 juin 1936. Soddy a également étendu le théorème aux sphères. Une solution géométrique est détaillée ici ^[6].

Définition de la courbure

Le théorème de Descartes s'énonce simplement en utilisant la courbure des cercles. La courbure d'un cercle est définie par ${\displaystyle k=\pm 1/r}$ , où r est son rayon. Plus le cercle est grand, plus sa courbure est petite, et vice versa.

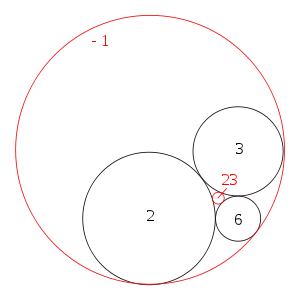
Le signe plus dans ${\displaystyle k=\pm 1/r}$ s'utilise pour un cercle qui est tangent extérieurement aux autres cercles, comme les trois cercles noirs dans la figure ci-dessus. Dans le cas d'un cercle tangent intérieurement, comme le grand cercle rouge dans la figure, on utilise le signe moins.

Le théorème de Descartes

Si quatre cercles tangents entre eux ont pour courbure ${\displaystyle k_{i}}$ (pour i = 1…4), le théorème de Descartes énonce^{[5],[4],[7],[8]}:

${\displaystyle (1)}$

${\displaystyle (k_{1}+k_{2}+k_{3}+k_{4})^{2}=2\,(k_{1}^{2}+k_{2}^{2}+k_{3}^{2}+k_{4}^{2}).}$

Une démonstration rapide datant de 2022 utilise le fait que le tétraèdre formé par les centres des quatre cercles a un volume donné par le déterminant de Cayley-Menger égal à 0^[9].

Cercles de Soddy

L'équation (1), vue comme une équation du second degré en ${\displaystyle k_{4}}$, permet d’obtenir la courbure des cercles tangents à trois cercles donnés tangents deux à deux :

${\displaystyle (2)}$

${\displaystyle k_{4}=k_{1}+k_{2}+k_{3}\pm 2{\sqrt {k_{1}k_{2}+k_{2}k_{3}+k_{3}k_{1}}}.}$

Le signe ± indique qu'il existe deux cercles solutions : ce sont les cercles de Soddy ; les deux courbures de ces cercles sont reliés par ${\displaystyle k_{4}+k'_{4}=2(k_{1}+k_{2}+k_{3})}$ ; on en déduit que si quatre de ces cinq courbures sont entières, la cinquième l'est aussi.

Cas particulier

Si l'un des trois cercles est remplacé par une droite, la courbure ${\displaystyle k_{3}}$ (par exemple) est nulle^[11]. Ainsi l'équation (2), nous donne :

${\displaystyle (3)}$

${\displaystyle k_{4}=k_{1}+k_{2}\pm 2{\sqrt {k_{1}k_{2}}}}$ ce qui s'écrit aussi : ${\displaystyle {\sqrt {k}}_{4}=|{\sqrt {k}}_{1}\pm {\sqrt {k}}_{2}|}$.

Le théorème de Descartes ne s'applique pas lorsque plus d'un cercle est remplacé par une droite.

Le théorème ne s'applique pas non plus lorsque plus d'un cercle est tangent intérieurement, par exemple dans le cas de trois cercles imbriqués tangents en un point.

Théorème complexe de Descartes

Afin de définir un cercle complètement, non seulement son rayon (ou sa courbure), mais aussi son centre doivent être connus. L'équation appropriée est plus claire si les coordonnées (x, y) sont interprétées comme un nombre complexe ${\displaystyle z=x+\mathrm {i} y.}$ L'équation est alors similaire au théorème de Descartes et s'appelle le théorème complexe de Descartes.

Soient quatre cercles de courbure ${\displaystyle k_{i}}$ et de centre ${\displaystyle z_{i}}$ (pour i = 1…4), l'égalité suivante se tire de l'équation (1):

${\displaystyle (4)}$

${\displaystyle (k_{1}z_{1}+k_{2}z_{2}+k_{3}z_{3}+k_{4}z_{4})^{2}=2\,(k_{1}^{2}z_{1}^{2}+k_{2}^{2}z_{2}^{2}+k_{3}^{2}z_{3}^{2}+k_{4}^{2}z_{4}^{2}).}$

Une fois ${\displaystyle k_{4}}$ trouvée via l'équation (2), on peut calculer ${\displaystyle z_{4}}$ en réécrivant l'équation (4) sous une forme semblable à l'équation (2). Encore une fois, il y aura en général deux solutions pour ${\displaystyle z_{4}}$, correspondant aux deux solutions pour ${\displaystyle k_{4}}$.

Notes et références

Voir aussi

Articles connexes

• Cercle de Ford
• Cercle d'Apollonius
• Problème des contacts
• Chaîne de Steiner
• Hexlet de Soddy

Liens externes

• (en) Soddy Circles and David Eppstein's Centers: What Are They? sur cut-the-knot : applet java interactive montrant quatre cercles tangents

• Portail de la géométrie