Shannon–Fano–Elias coding

In information theory, Shannon–Fano–Elias coding is a precursor to arithmetic coding, in which probabilities are used to determine codewords.^[1] It is named for Claude Shannon, Robert Fano, and Peter Elias.

Algorithm description

Given a discrete random variable X of ordered values to be encoded, let ${\displaystyle p(x)}$ be the probability for any x in X. Define a function

${\displaystyle {\bar {F}}(x)=\sum _{x_{i}<x}p(x_{i})+{\frac {1}{2}}p(x)}$

Algorithm:

For each x in X,

Let Z be the binary expansion of ${\displaystyle {\bar {F}}(x)}$.

Choose the length of the encoding of x, ${\displaystyle L(x)}$, to be the integer ${\displaystyle \left\lceil \log _{2}{\frac {1}{p(x)}}\right\rceil +1}$

Choose the encoding of x, ${\displaystyle code(x)}$, be the first ${\displaystyle L(x)}$ most significant bits after the decimal point of Z.

Example

Let X = {A, B, C, D}, with probabilities p = {1/3, 1/4, 1/6, 1/4}.

For A

${\displaystyle {\bar {F}}(A)={\frac {1}{2}}p(A)={\frac {1}{2}}\cdot {\frac {1}{3}}=0.1666\ldots }$

In binary, Z(A) = 0.0010101010...

${\displaystyle L(A)=\left\lceil \log _{2}{\frac {1}{\frac {1}{3}}}\right\rceil +1=\mathbf {3} }$

code(A) is 001

For B

${\displaystyle {\bar {F}}(B)=p(A)+{\frac {1}{2}}p(B)={\frac {1}{3}}+{\frac {1}{2}}\cdot {\frac {1}{4}}=0.4583333\ldots }$

In binary, Z(B) = 0.01110101010101...

${\displaystyle L(B)=\left\lceil \log _{2}{\frac {1}{\frac {1}{4}}}\right\rceil +1=\mathbf {3} }$

code(B) is 011

For C

${\displaystyle {\bar {F}}(C)=p(A)+p(B)+{\frac {1}{2}}p(C)={\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{2}}\cdot {\frac {1}{6}}=0.66666\ldots }$

In binary, Z(C) = 0.101010101010...

${\displaystyle L(C)=\left\lceil \log _{2}{\frac {1}{\frac {1}{6}}}\right\rceil +1=\mathbf {4} }$

code(C) is 1010

For D

${\displaystyle {\bar {F}}(D)=p(A)+p(B)+p(C)+{\frac {1}{2}}p(D)={\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{6}}+{\frac {1}{2}}\cdot {\frac {1}{4}}=0.875}$

In binary, Z(D) = 0.111

${\displaystyle L(D)=\left\lceil \log _{2}{\frac {1}{\frac {1}{4}}}\right\rceil +1=\mathbf {3} }$

code(D) is 111

Algorithm analysis

Prefix code

Shannon–Fano–Elias coding produces a binary prefix code, allowing for direct decoding.

Let bcode(x) be the rational number formed by adding a decimal point before a binary code. For example, if code(C) = 1010 then bcode(C) = 0.1010. For all x, if no y exists such that

${\displaystyle \operatorname {bcode} (x)\leq \operatorname {bcode} (y)<\operatorname {bcode} (x)+2^{-L(x)}}$

then all the codes form a prefix code.

By comparing F to the CDF of X, this property may be demonstrated graphically for Shannon–Fano–Elias coding.

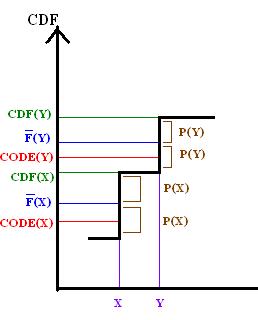
By definition of L it follows that

${\displaystyle 2^{-L(x)}\leq {\frac {1}{2}}p(x)}$

And because the bits after L(y) are truncated from F(y) to form code(y), it follows that

${\displaystyle {\bar {F}}(y)-\operatorname {bcode} (y)\leq 2^{-L(y)}}$

thus bcode(y) must be no less than CDF(x).

So the above graph demonstrates that the ${\displaystyle \operatorname {bcode} (y)-\operatorname {bcode} (x)>p(x)\geq 2^{-L(x)}}$, therefore the prefix property holds.

Code length

The average code length is ${\displaystyle LC(X)=\sum _{x\in X}p(x)L(x)=\sum _{x\in X}p(x)\left(\left\lceil \log _{2}{\frac {1}{p(x)}}\right\rceil +1\right)}$.
Thus for H(X), the entropy of the random variable X,

${\displaystyle H(X)+1\leq LC(X)<H(X)+2}$

Shannon Fano Elias codes from 1 to 2 extra bits per symbol from X than entropy, so the code is not used in practice.

See also

• Shannon–Fano coding

References