Simsonsche Gerade

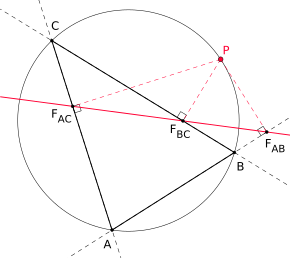
Die simsonsche Gerade ist ein Gegenstand der Dreiecksgeometrie. Liegen die Fußpunkte der von einem Punkt ${\displaystyle P}$ aus gefällten Lote auf die (eventuell verlängerten) Seiten eines Dreiecks ${\displaystyle \triangle ABC}$ auf einer gemeinsamen Geraden, so wird diese Gerade als simsonsche Gerade oder wallacesche Gerade und der Punkt ${\displaystyle P}$ als ihr Pol bezeichnet. Dies ist genau dann der Fall, wenn ${\displaystyle P}$ auf dem Umkreis von ${\displaystyle \triangle ABC}$ liegt.

Die Simson-Gerade ist irrtümlicherweise nach dem Mathematiker Robert Simson (1687–1768) benannt, in dessen Werk sich jedoch keine Arbeit zur Simson-Geraden finden lässt. In Wirklichkeit wurde sie 1797 von William Wallace (1768–1843) entdeckt.^[1]

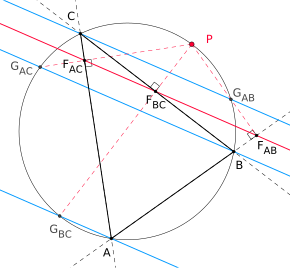Jede Simson-Gerade eines Dreieckes besitzt drei besondere Parallelen, die jeweils durch einen der drei Eckpunkte des Dreiecks verlaufen. Genauer gesagt gilt der folgende Satz: Gegeben sind ein Dreieck ${\displaystyle \triangle ABC}$, ein Punkt ${\displaystyle P}$ auf seinem Umkreis und die zugehörige Simson-Gerade. Ist GAB nun der Schnittpunkt des Lotes von ${\displaystyle P}$ auf ${\displaystyle AB}$ mit dem Umkreis, dann ist die Gerade CGAB parallel zur Simson-Geraden.[1]

Betrachtet man bei einem Dreieck zwei unterschiedliche Punkte auf dessen Umkreis, so erhält man zwei verschiedene Simson-Geraden. Der Schnittwinkel dieser beiden Simson-Geraden ist genau halb so groß wie der Winkel, den die beiden Punkte mit dem Mittelpunkt des Umkreises bilden. Es seien ${\displaystyle P_{1}}$ und ${\displaystyle P_{2}}$ zwei Punkte auf dem Umkreis von ${\displaystyle \triangle ABC}$ mit Mittelpunkt ${\displaystyle O}$. Weiterhin sei ${\displaystyle \alpha }$ der Schnittwinkel der beiden zugehörigen Simson-Geraden und ${\displaystyle \beta =\angle P_{1}OP_{2}}$. Dann gilt ${\displaystyle 2\alpha =\beta }$.[1]

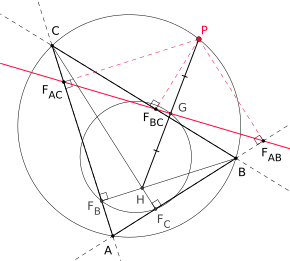Verbindet man den Höhenschnittpunkt eines Dreiecks mit einem Punkt auf dem Umkreis des Dreiecks, so wird diese Verbindungsstrecke von der zugehörigen Simson-Geraden halbiert. Gegeben sind ein Dreieck ${\displaystyle \triangle ABC}$, ein Punkt ${\displaystyle P}$ auf seinem Umkreis und die zugehörige Simson-Gerade. Ist H der Höhenschnittpunkt von ${\displaystyle \triangle ABC}$, dann schneidet die Simson-Gerade die Strecke ${\displaystyle {\overline {HP}}}$ in ${\displaystyle G}$ und es gilt ${\displaystyle |HG|=|GP|}$. Außerdem liegt ${\displaystyle G}$ auf dem Feuerbachkreis.[1][2]

Lässt man den Simson-Pol ${\displaystyle P}$ auf dem Kreis wandern, dann besitzt die so entstehende Geradenschar von Simson-Geraden eine Deltoide, auch als Steiner-Hypozykloide bezeichnet, als Hüllkurve.[1][2]

Besitzen zwei Dreiecke denselben Umkreis und ihre zugehörigen Simson-Geraden denselben Pol, so ist der Schnittwinkel der beiden Simson-Geraden unabhängig von der Wahl des Pols. Mit anderen Worten: Für alle Punkte ${\displaystyle P}$ auf dem gemeinsamen Umkreis der beiden Dreiecke ergibt sich ein gleich großer Schnittwinkel der beiden zugehörigen Simson-Geraden.

Die Simson-Gerade beziehungsweise eine auf ihr liegende Strecke lässt sich auch als entartetes Fußpunktdreieck auffassen. Verbindet man die Fußpunkte eines Punktes in der Ebene, so erhält im Normalfall ein Dreieck. Nähert sich der Punkt in der Ebene dem Umkreis des Ausgangsdreiecks an, dann geht das Fußpunktdreieck in eine Strecke auf der Simson-Gerade über.

Bewiesen wird: Liegt ${\displaystyle P}$ auf dem Umkreis von ${\displaystyle \triangle ABC}$, so liegen die Fußpunkte auf einer gemeinsamen Geraden. Dazu zeigt man, dass ${\displaystyle \angle EFP+\angle PFD=180^{\circ }}$ gilt.

Die Fußpunkte ${\displaystyle E}$ und ${\displaystyle F}$ liegen auf dem Thaleskreis über ${\displaystyle [PA]}$. Da Umfangswinkel (Peripheriewinkel) über demselben Kreisbogen gleich groß sind, folgt

${\displaystyle {\begin{aligned}\angle EFP&=90^{\circ }+\angle EFA=90^{\circ }+\angle EPA\\&=90^{\circ }+(90^{\circ }-\angle PAC)=180^{\circ }-\angle PAC\end{aligned}}}$.

Andererseits ist ${\displaystyle PBCA}$ voraussetzungsgemäß ein Sehnenviereck. Die gegenüberliegenden Winkel ${\displaystyle \angle PAC}$ und ${\displaystyle \angle CBP}$ dieses Vierecks ergänzen sich daher zu ${\displaystyle 180^{\circ }}$. Insgesamt ergibt sich also

${\displaystyle \angle EFP=\angle CBP}$.

Die Punkte ${\displaystyle D}$ und ${\displaystyle F}$ liegen auf dem Thaleskreis über ${\displaystyle [PB]}$, sodass auch ${\displaystyle PBDF}$ ein Sehnenviereck ist. Ähnlich wie vorher schließt man ${\displaystyle \angle PFD=\angle DBP}$. Wegen ${\displaystyle \angle DBP+\angle CBP=180^{\circ }}$ erhält man daraus

${\displaystyle {\begin{aligned}\angle PFD&=90^{\circ }-\angle DFB=90^{\circ }-(90^{\circ }-\angle PBD)\\&=\angle PBD=180^{\circ }-\angle CBP\end{aligned}}}$.

Damit ist mit

${\displaystyle \angle EFP+\angle PFD=\angle CBP+(180^{\circ }-\angle CBP)=180^{\circ }}$

die Behauptung bewiesen.

Bemerkung: Der angegebene Beweis bezieht sich auf die in der Skizze dargestellte Lage der Höhenfußpunkte. Liegen diese anders, muss die Begründung entsprechend variiert werden.

1. ↑ ^{a b c d e} H. S. M. Coxeter, S. L. Greitzer: Simson Lines. § 2.5 in Geometry Revisited. In: Math. Assoc. Amer., Washington DC 1967, S. 41.
2. ↑ ^{a b} Eric W. Weisstein: Simson-Gerade (engl.). In: MathWorld (englisch).

• Max Koecher, Aloys Krieg: Ebene Geometrie. 3. Auflage. Springer-Verlag, Berlin 2007, ISBN 978-3-540-49327-3, S. 170–172.
• H. S. M. Coxeter, S. L. Greitzer: Zeitlose Geometrie. Klett, Stuttgart 1983.
• Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007, ISBN 978-0-486-46237-0, S. 137 ff., 206 ff., 243, 251 (Erstveröffentlichung 1929 bei der Houghton Mifflin Company (Boston) unter dem Titel Modern Geometry).
• Ross Honsberger: Episodes in Nineteenth and Twentieth Century Euclidean Geometry. MAA, 1995, S. 43–48, 82–83, 121, 128–136.

Commons: Simson-Gerade – Sammlung von Bildern, Videos und Audiodateien

• Simson-Gerade auf geogebra.org (interaktive Illustration)
• Eric W. Weisstein: Simson-Gerade (engl.). In: MathWorld (englisch).
• Simson-Gerade auf Matroids Matheplanet
• Simson-Gerade (PDF; 48 kB) matheraetsel.de
• Simson-Gerade (englisch) cut-the-knot.org