Einfeldträger

Der Einfeldträger oder auch Träger auf zwei Stützen ist das einfachste statische Element. Er ist das Grundelement vieler Brücken und Gebäude und wird in der Technischen Mechanik häufig als Übungsbeispiel verwendet.

Der Träger ist statisch bestimmt. Unter Belastung entstehen in den beiden Lagern drei Auflagerreaktionen. Die Auflagerkräfte können ohne aufwändige Rechenverfahren ermittelt werden.

Äußere Kräfte

Auflagereaktionen

${\displaystyle A_{v}}$	vertikale Auflagerreaktion in Auflager A (Festlager; Gelenklager)
${\displaystyle A_{h}}$	horizontale Auflagereaktion in Auflager A
${\displaystyle B_{v}}$	vertikale Auflagerreaktion in Auflager B (Loslager; Rollenlager)
${\displaystyle B_{h}=0}$	horizontale Auflagerreaktion in Auflager B (verschwindet, da reibungsfrei beweglich gelagert)

Lasten

${\displaystyle F_{n}}$	äußere Kräfte ${\displaystyle F_{1}}$, ${\displaystyle F_{2}}$ usw.
${\displaystyle M_{n}}$	äußere Momente ${\displaystyle M_{1}}$, ${\displaystyle M_{2}}$ usw.
${\displaystyle q}$	Streckenlast

Innere Kräfte (Schnittgrößen)

${\displaystyle N_{x}}$	Normalkraft im Balken
${\displaystyle Q_{z}}$	Querkraft im Balken
${\displaystyle M_{y}}$	Moment im Balken

Gleichgewichtsbedingungen

Alle äußeren Lasten und alle Auflagerkräfte sind im Gleichgewicht.

• Summe aller Vertikalkräfte: z. B. ${\displaystyle \sum F_{v}=0=F_{1,z}+F_{2,z}+A_{v}+B_{v}}$
• Summe aller Horizontalkräfte: z. B. ${\displaystyle \sum F_{h}=0=F_{1,x}+F_{2,x}+A_{h}}$
• Summe aller Momente: z. B. ${\displaystyle \sum M_{A}=0=F_{1,z}\cdot x_{1}+F_{2,z}\cdot x_{2}+B_{v}\cdot L}$

In den drei Formeln sind drei Unbekannte enthalten ${\displaystyle A_{v}}$, ${\displaystyle A_{h}}$, ${\displaystyle B_{v}}$, die nach mathematischen Regeln lösbar sind. Es sind die Vorzeichen allerdings strikt zu beachten. Hier und in der oberen Skizze sind positiv: Vertikale Kräfte von oben nach unten, Horizontale Kräfte von links nach rechts, rechtsdrehende Momente.

Maximales Biegemoment bei Gleichlast

Als maximales Biegemoment eines Einfeldträgers mit Gleichlast ergibt sich:

${\displaystyle M_{\mathrm {max} }={\frac {q\cdot l^{2}}{8}}}$

Formelsymbole

${\displaystyle M_{\mathrm {max} }}$	maximales Biegemoment in Feldmitte [kNm]
${\displaystyle q}$	Streckenlast [kN/m]
${\displaystyle l}$	Stützweite des Trägers [m]

Mit dieser Formel lassen sich auch viele andere statische Systeme in guter Näherung (auf der sicheren Seite) berechnen. Sie wird daher gerne für Überschlagsrechnungen ohne EDV-Unterstützung verwendet. Für den gelenkig gelagerten Einfeldträger mit Gleichlast ist die Formel allerdings eine exakte Lösung. Die Momentenlinie bildet dabei immer eine Parabel.

Herleitung:

Aus den Summenformeln für horizontale und vertikale Kräfte ergibt sich folgendes:

${\displaystyle A_{h}=0\,}$

${\displaystyle A_{v}=B_{v}={\frac {q\cdot l}{2}}}$

Die x-Achse wird in diesem Fall von links und in A beginnend angenommen:

${\displaystyle M(x)=A_{v}\cdot x-q\cdot x\cdot {\frac {x}{2}}}$

${\displaystyle M(x)=q\cdot l\cdot {\frac {x}{2}}-q\cdot {\frac {x^{2}}{2}}}$

Das Maximalmoment ist immer an der Stelle, wo die erste Ableitung der Momentenlinie null ist. Die erste Ableitung von M(x) nach x ergibt folgende Formel:

${\displaystyle M'(x)=q\cdot {\frac {l}{2}}-q\cdot x}$

Nullsetzen der Formel ergibt einen x-Wert für die Stelle des lokalen Maximums:

${\displaystyle 0=q\cdot {\frac {l}{2}}-q\cdot x}$

${\displaystyle x={\frac {l}{2}}}$

Durch Einsetzen dieses Wertes in M(x) erhält man:

${\displaystyle M(x)=M_{\mathrm {max} }={\frac {q\cdot l^{2}}{8}}}$

Parabelstich

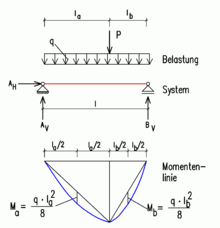
Die obige Formel kann ebenfalls dazu verwendet werden, den Parabelstich zu ermitteln, wenn neben einer Gleichlast auch einzelne Lasten auftreten (Knick in der Momentenlinie).

Siehe auch

• Träger (Architektur)
• Balkentheorie
• Statische Berechnung

Literatur

• A. Goris (Hrsg.): Schneider Bautabellen für Ingenieure. 20. Auflage. Werner Verlag, Köln 2012, ISBN 978-3-8041-5251-9, S. 4.2 ff.