Automatisches Differenzieren

Das automatische Differenzieren bzw. Differenzieren von Algorithmen ist ein Verfahren der Informatik und angewandten Mathematik. Zu einer Funktion in mehreren Variablen, die als Prozedur in einer Programmiersprache oder als Berechnungsgraph gegeben ist, wird eine erweiterte Prozedur erzeugt, die sowohl die Funktion als auch einen oder beliebig viele Gradienten bis hin zur vollen Jacobi-Matrix auswertet. Wenn das Ausgangsprogramm Schleifen enthält, darf die Anzahl der Schleifendurchläufe nicht von den unabhängigen Variablen abhängig sein.

Diese Ableitungen werden z. B. für das Lösen von nichtlinearen Gleichungssystemen mittels Newton-Verfahren und für Methoden der nichtlinearen Optimierung benötigt.

Das wichtigste Hilfsmittel dabei ist die Kettenregel sowie die Tatsache, dass zu den im Computer verfügbaren Elementarfunktionen wie sin, cos, exp, log die Ableitungen bekannt und genauso exakt berechenbar sind. Damit wird der Aufwand zur Berechnung der Ableitungen proportional (mit kleinem Faktor) zum Aufwand der Auswertung der Ausgangsfunktion.

Berechnung von Ableitungen

Aufgabe: Gegeben sei eine Funktion

${\displaystyle f\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m},x\mapsto y}$

Gesucht ist der Code/die Funktion für Richtungsableitungen oder die volle Jacobi-Matrix

${\displaystyle {\frac {\partial f}{\partial x}}=\left[{\tfrac {\partial y_{i}}{\partial x_{j}}}\right]_{i=1..m,j=1..n}}$

Verschiedene Ansätze hierfür sind:

1. Versuche, eine geschlossene, analytische Form für f zu finden und bestimme ${\displaystyle {\tfrac {\partial f}{\partial x}}}$ durch Differentiation „auf Papier“. Implementiere dann den Code für ${\displaystyle {\tfrac {\partial f}{\partial x}}}$ von Hand.

   Problem: Zu schwierig, zeitaufwendig, fehleranfällig

   Vorteile: sehr effizient, hohe Genauigkeit

2. Erzeuge die Berechnungsvorschrift für f in einem Computeralgebrasystem und wende die dort zur Verfügung stehenden Mittel zum symbolischen Differenzieren an. Exportiere dann den Code für ${\displaystyle {\tfrac {\partial f}{\partial x}}}$ in seine eigentliche Umgebung.

   Problem: Zeitaufwendig, skaliert nicht, zu kompliziert für größere Programme/Funktionen

3. Bestimme eine numerische Approximation der Ableitung. Es gilt für kleines h

   ${\displaystyle {\tfrac {\partial f_{k}}{\partial x}}=\lim _{h\to 0}{\frac {f_{k}(x+h)-f_{k}(x)}{h}}\approx {\frac {f_{k}(x+h)-f_{k}(x)}{h}}}$.

   Problem: Wahl der optimalen Schrittweite h, ungenau, eventuell Instabilität

   Vorteil: einfache Berechnung

4. Stelle die Berechnungsvorschrift als Berechnungsbaum, d. h. als arithmetisches Netzwerk, dar und erweitere diesen unter Verwendung der Kettenregel zu einem Berechnungsbaum für Funktionswert und Ableitung ${\displaystyle {\tfrac {\partial f}{\partial x}}}$.

Die Idee der automatischen Differentiation (AD)

Eine Funktion ${\displaystyle f(x)\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m},x\mapsto y}$ kann als eine Verkettung elementarer Teil-Funktionen beschrieben werden. Automatische Differentiation (AD) berechnet die Ableitung als Verkettung partieller Ableitungen. AD benötigt daher den Wert und die Ableitung jeder Teil-Funktion als Zwischenergebnis. Dem Zwischenwert jeder Teil-Funktion wird nachfolgend eine Variable ${\displaystyle (t_{1},t_{2},t_{3},\dots )}$ zugewiesen. Man kann sich dies so vorstellen, dass es eine (potentiell unendliche) Folge von Zwischenwerten ${\displaystyle (t_{1},t_{2},t_{3},\dots )}$ gibt und Funktionen ${\displaystyle q_{k}\colon \mathbb {R} ^{n+k-1}\to \mathbb {R} }$, die aber nur von ein oder zwei Variablen wirklich abhängen. Die Funktion wird ausgewertet, indem am Anfang ${\displaystyle (t_{1},t_{2},\dots ,t_{n})=(x_{1},x_{2},\dots ,x_{n})}$ gesetzt wird und nacheinander

${\displaystyle {\begin{aligned}t_{n+1}=&q_{1}(t_{1},\dots ,t_{n})\\t_{n+2}=&q_{2}(t_{1},\dots ,t_{n},t_{n+1})\\\dots &\\t_{n+K}=&q_{K}(t_{1},\dots ,t_{n},t_{n+1},\dots ,t_{K-1})\end{aligned}}}$

bestimmt wird. Dies kann so eingerichtet werden, dass die Funktionswerte von f sich in den zuletzt ausgewerteten Zwischenergebnissen befinden, d. h. am Ende wird noch ${\displaystyle (y_{1},\dots ,y_{m})=(t_{K-m+1},\dots ,t_{K})}$ zugeordnet.

AD beschreibt eine Menge von Verfahren, deren Ziel es ist, ein neues Programm zu erzeugen, das die Jacobimatrix von f, ${\displaystyle J={\tfrac {\partial f}{\partial x}}\in \mathbb {R} ^{m\times n}}$ auswertet. Die Eingabevariablen x heißen unabhängige Variablen, die Ausgabevariable(n) y abhängige Variablen. Bei AD unterscheidet man mindestens zwei verschiedene Modi.

1. Vorwärtsmodus (engl. Forward Mode)
2. Rückwärtsmodus (engl. Reverse Mode)

Beide Modi basieren auf der Kettenregel, wonach die Ableitung einer Funktion sich als Verkettung partieller Ableitungen darstellen lässt: ${\displaystyle {\frac {\partial f(g)}{\partial x}}={\frac {\partial f(g)}{\partial g}}\cdot {\frac {\partial g}{\partial x}}}$. Der Vorwärtsmodus beginnt mit der inneren Ableitung ${\displaystyle {\frac {\partial g}{\partial x}}}$, der Rückwärtsmodus mit der äußeren ${\displaystyle {\frac {\partial f(g)}{\partial g}}}$. Der Wert der partiellen Ableitung, genannt Saat (engl. seed), wird jeweils vor- bzw. zurückpropagiert und ist initial ${\displaystyle {\frac {\partial x}{\partial x}}=1}$ bzw. ${\displaystyle {\frac {\partial f(g)}{\partial f(g)}}=1}$. Der Vorwärtsmodus wertet im selben Schritt die Funktion aus und berechnet die Ableitung bzgl. einer unabhängigen Variablen. Für jede unabhängige Variable ${\displaystyle x_{1},x_{2},\dots ,x_{n}}$ ist daher ein eigener Schritt nötig, in dem die Ableitung bzgl. einer unabhängigen Variable auf eins (${\displaystyle {\frac {\partial x_{1}}{\partial x_{1}}}=1}$) und aller anderen auf null (${\displaystyle {\frac {\partial x_{2}}{\partial x_{1}}}=\dots ={\frac {\partial x_{n}}{\partial x_{1}}}=0}$) gesetzt wird. Im Gegensatz dazu benötigt der Rückwärtsmodus für die partiellen Ableitungen die ausgewerteten Teil-Funktionen. Der Rückwärtsmodus wertet daher die Funktion zuerst aus und berechnet die Ableitungen bzgl. aller unabhängiger Variablen in einem zusätzlichen Rückwärtsschritt.

Vorwärtsmodus

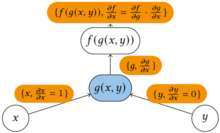
Im Vorwärtsmodus werden die partiellen Ableitungen entlang des Kontrollflusses der Berechnung von f transportiert, also von der innersten zur äußersten partiellen Ableitung.

Beispiel

Berechne eine Funktion ${\displaystyle f(x_{1},x_{2},a)=(x_{1}+x_{2})\cdot a\cdot \sin(x_{1}+x_{2})=y_{2}}$

 ${\displaystyle {\begin{aligned}&[y_{0},y_{1},y_{2}]=f\left(x_{1},x_{2},a\right)\left\{\right.\\&\quad y_{0}=x_{1}+x_{2}\\&\quad y_{1}=a\cdot \sin(y_{0})\\&\quad y_{2}=y_{0}\cdot y_{1}\\&\left.\right\}\end{aligned}}}$

Eine automatische Differentiation im Vorwärtsmodus hätte eine Funktion

 ${\displaystyle [y_{0},y_{1},y_{2},y_{0}',y_{1}',y_{2}']=f_{AD}\left(x_{1},x_{2},x_{1}',x_{2}',a\right)}$

zum Ergebnis, die den Wert der inneren Ableitung von ${\displaystyle x_{1},x_{2}}$ (${\displaystyle x_{1}',x_{2}'}$) erwartet und die Ableitung von ${\displaystyle y_{0},y_{1},y_{2}}$ (${\displaystyle y_{0}',y_{1}',y_{2}'}$) zurückgibt:

 ${\displaystyle {\begin{aligned}&[y_{0},y_{1},y_{2},y_{0}',y_{1}',y_{2}']=f_{AD}\left(x_{1},x_{2},x_{1}',x_{2}',a\right)\left\{\right.\\&\quad y_{0}=x_{1}+x_{2}\\&\quad y_{0}'=x_{1}'+x_{2}'\\&\quad y_{1}=a\cdot \sin(y_{0})\\&\quad y_{1}'=a\cdot \cos(y_{0})\cdot y_{0}'\\&\quad y_{2}=y_{0}\cdot y_{1}\\&\quad y_{2}'=y_{0}'\cdot y_{1}+y_{0}\cdot y_{1}'\\&\left.\right\}\end{aligned}}}$

Um die Ableitung ${\displaystyle {\frac {\partial y_{2}}{\partial x_{1}}}}$ zu berechnen, muss ${\displaystyle {\frac {\partial x_{1}}{\partial x_{1}}}=x_{1}'=1}$ und ${\displaystyle {\frac {\partial x_{2}}{\partial x_{1}}}=x_{2}'=0}$ gesetzt werden und entsprechend für ${\displaystyle {\frac {\partial y_{2}}{\partial x_{2}}}}$ dann ${\displaystyle {\frac {\partial x_{1}}{\partial x_{2}}}=x_{1}'=0}$ und ${\displaystyle {\frac {\partial x_{2}}{\partial x_{2}}}=x_{2}'=1}$.

Deutlich intuitiver ist, die Funktion rekursiv anhand ihrer Teilfunktionen zu berechnen. Dabei gibt der modifizierte Funktionsaufruf ein Zweier-Tupel aus dem Wert der Funktion und der partiellen Ableitung zurück und erwartet als Argument den Wert aller Variablen und der partiellen Ableitung aller unabhängigen Variablen:

 ${\displaystyle {\begin{aligned}(y_{0},y_{0}')&=y_{0_{AD}}(x_{1},x_{2},x_{1}',x_{2}')=(x_{1}+x_{2},x_{1}'+x_{2}'),\\(y_{1},y_{1}')&=y_{1_{AD}}(a,y_{0},y_{0}')=(a\cdot \sin(y_{0}),a\cdot \cos(y_{0})\cdot y_{0}'),\\(y_{2},y_{2}')&=y_{2_{AD}}(y_{0},y_{1},y_{0}',y_{2})=(y_{0}\cdot y_{1},y_{0}'\cdot y_{1}+y_{0}\cdot y_{1}').\\\end{aligned}}}$

Pseudocode

Der Vorwärtsmodus berechnet die Funktion und die Ableitung (aber jeweils nur für eine unabhängige Variable) in einem Schritt. Der zugehörige Methodenaufruf erwartet den abzuleitenden Ausdruck Z und die Variable V, nach der abgeleitet wird. Die Methode gibt ein Wertepaar aus der ausgewerteten Funktion und der zugehörigen Ableitung zurück. Die Methode arbeitet den Ausdrucksbaum rekursiv ab, bis eine Variable erreicht wird. Ist das die Variable, nach der abgeleitet wird, so ist deren Ableitung 1, 0 anderenfalls. Anschließend werden die partielle Funktion sowie die partielle Ableitung ausgewertet.^[1]

tuple<float,float> auswerten(Ausdruck Z, Ausdruck V) {
   if istVariable(Z)
      if (Z=V) return {wertVon(Z),1};
      else return {wertVon(Z),0};
   else if (Z = X + Y)
      {x,x'} = auswerten(X,V);
      {y,y'} = auswerten(Y,V);
      return {x+y, x'+y'};
   else if (Z = X - Y)
      {x,x'} = auswerten(X,V);
      {y,y'} = auswerten(Y,V);
      return {x-y, x'-y'};
   else if (Z = X * Y)
      {x,x'} = auswerten(X,V);
      {y,y'} = auswerten(Y,V);
      return {x*y, x'*y+x*y'};
}

Rückwärtsmodus

Der Rückwärtsmodus besteht aus zwei Phasen.

1. Das Originalprogramm wird ausgeführt und die Werte der ausgewerteten Teil-Funktionen zwischengespeichert.
2. Das Originalprogramm wird rückwärts ausgeführt. Dabei werden die äußeren partiellen Ableitungen zur Berechnung der inneren verwendet. Dabei werden die Werte aus Phase 1 verwendet.

Beispiel

Zuerst werden die Teil-Funktionen der Funktion ${\displaystyle f(x_{1},x_{2},a)=(x_{1}+x_{2})\cdot a\cdot \sin(x_{1}+x_{2})=y_{2}}$ ausgewertet:

${\displaystyle {\begin{aligned}y_{0}&=x_{1}+x_{2}&&(1)\\y_{1}&=a\cdot \sin(y_{0})&&(2)\\y_{2}&=y_{0}\cdot y_{1}&&(3)\\\end{aligned}}}$

Anschließend wird die äußerste partielle Ableitung ${\displaystyle {\frac {\partial y_{2}}{\partial y_{1}}}}$ ${\displaystyle (4)}$ gebildet, um daraus die inneren Ableitungen zu berechnen. Für die Ableitung ${\displaystyle {\frac {\partial y_{2}}{\partial y_{0}}}}$ muss man berücksichtigen, dass ${\displaystyle y_{0}}$ in ${\displaystyle (2)}$ und ${\displaystyle (3)}$ vorkommt: aus ${\displaystyle (2)}$ stammt der Teil ${\displaystyle y_{0}\cdot (a\cdot \cos(y_{0}))}$, aus ${\displaystyle (3)}$ der Teil ${\displaystyle y_{1}}$, die beide addiert werden.

${\displaystyle {\begin{aligned}{\frac {\partial y_{2}}{\partial y_{1}}}&={\frac {\partial y_{2}}{\partial y_{2}}}\cdot {\frac {\partial y_{2}}{\partial y_{1}}}=1\cdot y_{0}=y_{0}&(4)\\{\frac {\partial y_{2}}{\partial y_{0}}}&={\frac {\partial y_{2}}{\partial y_{1}}}\cdot {\frac {\partial y_{1}}{\partial y_{0}}}=y_{0}\cdot (a\cdot \cos(y_{0}))+y_{1}&(5)\\{\frac {\partial y_{2}}{\partial x_{1}}}&={\frac {\partial y_{2}}{\partial y_{0}}}\cdot {\frac {\partial y_{0}}{\partial x_{1}}}=(y_{0}\cdot (a\cdot \cos(y_{0}))+y_{1})\cdot 1&(6)\\{\frac {\partial y_{2}}{\partial x_{2}}}&={\frac {\partial y_{2}}{\partial y_{0}}}\cdot {\frac {\partial y_{0}}{\partial x_{2}}}=(y_{0}\cdot (a\cdot \cos(y_{0}))+y_{1})\cdot 1&(7)\\\end{aligned}}}$

Aufgrund der Distributivität könnte man ${\displaystyle x_{1},x_{2},y_{0}}$ in ${\displaystyle x_{1}=x_{11}+x_{12}}$, ${\displaystyle x_{2}=x_{21}+x_{22}}$ und ${\displaystyle y_{01}=x_{11}+x_{21},y_{02}=x_{12}+x_{22}}$ aufteilen mit ${\displaystyle {\frac {\partial y_{2}}{\partial x_{1}}}={\frac {\partial y_{2}}{\partial x_{11}}}+{\frac {\partial y_{2}}{\partial x_{12}}},{\frac {\partial y_{2}}{\partial x_{2}}}={\frac {\partial y_{2}}{\partial x_{21}}}+{\frac {\partial y_{2}}{\partial x_{22}}}}$.

Pseudocode

Der Rückwärtsmodus berechnet alle Komponente der Jacobi-Matrix in zwei Schritten: Im Vorwärtsschritt wird zuerst die Funktion ausgewertet und die partiellen Ergebnisse zwischengespeichert. Im Rückwärtsschritt werden die partiellen Ableitungen berechnet und der zuvor abgeleitete Wert zurückpropagiert (backpropagation). Der zugehörige Methodenaufruf erwartet den abzuleitenden Ausdruck Z und seed mit dem abgeleiteten Wert des Elternausdrucks. Für den obersten Ausdruck, Z nach Z abgeleitet, ist dieser 1. Die Methode arbeitet den Ausdrucksbaum rekursiv ab, bis eine Variable erreicht wird, und addiert den aktuellen seed-Wert zu dem Ausdruck für die Ableitung der Komponente.^[2][3]

void ableiten(Ausdruck Z, float seed) {
   if (Z = X + Y)
      ableiten(X,seed);
      ableiten(Y,seed);
   else if (Z = X - Y)
      ableiten(X,seed);
      ableiten(Y,-seed);
   else if (Z = X * Y)
      ableiten(X,wertVon(X)*seed);
      ableiten(Y,seed*wertVon(Y));
   else if istVariable(Z)
      partielleAbleitungVon(Z) += seed;
}

Effizienzbetrachtungen

Die Effizienz von AD-Algorithmen hängt vom Modus und dem Parameter p ab. Die Wahl des Modus und des Parameters p hängt davon ab, wofür die Jacobimatrix berechnet wird. Es bezeichne

${\displaystyle T_{f}}$	die Zeit f zu berechnen
${\displaystyle M_{f}}$	der Speicherbedarf dieser Rechnung
${\displaystyle T_{JS}}$	die Zeit f und JS zu berechnen
${\displaystyle M_{JS}}$	der Speicherbedarf dieser Rechnung
${\displaystyle T_{SJ}}$	die Zeit f und SJ zu berechnen
${\displaystyle M_{SJ}}$	der Speicherbedarf dieser Rechnung

Für die beiden vorgestellten Modi gilt

1. Vorwärtsmodus: ${\displaystyle {\frac {T_{JS}}{T_{f}}}\approx p,{\frac {M_{JS}}{M_{f}}}\approx p}$
2. Rückwärtsmodus: ${\displaystyle {\frac {T_{SJ}}{T_{f}}}\approx p,{\frac {M_{SJ}}{M_{f}}}\approx T_{f}}$

Der Vorwärtsmodus hat den Vorteil, dass keine Zwischenergebnisse für einen zweiten Durchgang gespeichert werden müssen, und den Nachteil, dass er pro Komponente einmal ausgeführt werden muss. Dennoch basieren beide AD-Algorithmen auf der Berechnung partieller Ableitungen. Ein Compiler ist daher in der Lage den Code des Vorwärtsmodus zu optimieren, sodass partielle Ableitungen, die für mehr als eine Komponente benötigt werden, auch nur einmal – wie im Rückwärtsmodus – berechnet werden.^[1]

Die Berechnung als Kette von Berechnungen

Gegeben: ${\displaystyle s=g\left(u,v\right)}$, Frage: Wie verändert sich die Ableitung von s während der zweiten Phase, um die Ableitungen von u und v zu erhalten?

${\displaystyle f(x)}$ wird als Sequenz von Programmen interpretiert. Im Beispiel „Optimierung eines Tragflügels“ umfasst die Berechnung die folgenden Schritte.

• Überlagerung des Tragflügels mit sogenannten „Mode-Funktionen“

${\displaystyle A\left(x\right)=A_{0}+\sum _{j=1}^{n}x_{j}A_{j},n=8,f_{1}:\mathbb {R} ^{8}\rightarrow \mathbb {R} ^{200}}$

• Berechnung eines Gitters, das um den Tragflügel herum gelegt wird

${\displaystyle G\left(A\right):\mathbb {R} ^{200}\rightarrow \mathbb {R} ^{17428}}$

• Lösung der Navier-Stokes-Gleichungen auf dem Gitter und Berechnung der Integrals der selbigen.

${\displaystyle f\left(G\right):\mathbb {R} ^{17428}\rightarrow \mathbb {R} }$

.

Insgesamt ergibt sich die Funktion

  ${\displaystyle f=f\left(G\left(A\left(x\right)\right)\right)\rightarrow {\frac {\partial f}{\partial x}}={\frac {\partial f}{\partial G}}{\frac {\partial G}{\partial A}}{\frac {\partial A}{\partial x}}}$

Mit einem naiven Ansatz würde man drei Matrizen ${\displaystyle {\frac {\partial f}{\partial G}}}$, ${\displaystyle {\frac {\partial G}{\partial A}}}$, ${\displaystyle {\frac {\partial A}{\partial x}}}$ berechnen und dann zwei Matrizenmultiplikationen durchführen. Der Nachteil des Vorwärtsmodus ist allerdings:

  ${\displaystyle T_{{\frac {\partial f}{\partial G}}\cdot S}\approx 17428\cdot T_{f\left(G\right)}}$

im Rückwärtsmodus würde analog

  ${\displaystyle T_{S\cdot {\frac {\partial f}{\partial G}}}\approx 17428\cdot T_{f\left(G\right)}}$

gelten. Ein besserer Ansatz ist, das Ergebnis einer Berechnung jeweils als Saatmatrix der folgenden einzusetzen.

1. Wähle ${\displaystyle I_{8x8}\in \mathbb {R} ^{8x8}}$ als Saatmatrix der ersten Rechnung
2. Das Ergebnis der ersten Rechnung als Saatmatrix der zweiten Rechnung
3. Das Ergebnis der zweiten Rechnung als Saatmatrix der dritten Rechnung

also

1. ${\displaystyle {\frac {\partial A}{\partial x}}I_{8\times 8}\in \mathbb {R} ^{8\times 200}}$
2. ${\displaystyle {\frac {\partial G}{\partial A}}{\frac {\partial A}{\partial x}}\in \mathbb {R} ^{8\times 17428}}$
3. ${\displaystyle {\frac {\partial f}{\partial G}}{\frac {\partial G}{\partial x}}\in \mathbb {R} ^{8\times 1}}$

Da die Zeilenzahl jeder Matrix 8 (p=8) ist, erhöht sich der Zeit- und Speicherbedarf gegenüber der regulären Auswertung von ${\displaystyle f(x)}$ um höchstens 8.

Literatur

• Andreas Griewank, Andrea Walther (2008): Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation, Second Edition, SIAM, xxii + 438 Seiten, ISBN 978-0-89871-659-7
• George F. Corliss; Andreas Griewank (1993): "Operator Overloading as an Enabling Technology for Automatic Differentiation" (PDF; 227 kB), Technical Report MCS-P358-0493, Mathematics and Computer Science Division, Argonne National Laboratory

Weblinks

• Portal autodiff.org mit Programmierwerkzeugen zum Thema
• Übersicht über Softwaretools

Einzelnachweise

1. ↑ ^{a b} Maximilian E. Schüle, Maximilian Springer, Alfons Kemper, Thomas Neumann,: LLVM Code Optimisation for Automatic Differentiation. In: DEEM '22: Proceedings of the Sixth Workshop on Data Management for End-To-End Machine Learning. 2022, doi:10.1145/3533028.3533302 (englisch). 
2. ↑ Maximilian E. Schüle, Harald Lang, Maximilian Springer, Alfons Kemper, Thomas Neumann, Stephan Günnemann: In-Database Machine Learning with SQL on GPUs. In: 33rd International Conference on Scientific and Statistical Database Management. 2021, doi:10.1145/3468791.3468840 (englisch). 
3. ↑ Maximilian E. Schüle, Harald Lang, Maximilian Springer, Alfons Kemper, Thomas Neumann, Stephan Günnemann: Recursive SQL and GPU-support for in-database machine learning. In: Distributed and Parallel Databases. 2022, doi:10.1007/s10619-022-07417-7 (englisch).