Äquidistante Hyperfläche

Eine Äquidistante Hyperfläche oder Parallele Hyperfläche ist in der Geometrie eine Hyperfläche, die in einem konstanten Abstand um eine Hyperfläche herumläuft. Dies verallgemeinert den Begriff der Parallelkurve, die in einem konstanten Abstand um eine Bezugslinie herumläuft. 2-dimensionale äquidistante Hyperflächen werden auch als Parallelflächen bezeichnet.

Die Funktion ${\displaystyle f:\mathbb {R} ^{n}\rightarrow \mathbb {R} ^{r}}$ sei stetig differenzierbar und habe eine reguläre Nullstellenmenge (diese ist dann eine ${\displaystyle n-r}$-dimensionale Untermannigfaltigkeit des ${\displaystyle R^{n}}$). Für hinreichend kleines ${\displaystyle d>0}$ ist die Äquidistante Hyperfläche ${\displaystyle A}$ mit Abstand ${\displaystyle d}$ von der Nullstellenmenge ${\displaystyle f^{-1}(0)}$ von  ${\displaystyle f}$ die Enveloppe der Sphärenschar ${\displaystyle {\big (}S_{d}({\bar {x}}){\big )}_{{\bar {x}}\in f^{-1}(0)}}$.

Die Sphärenschar wird durch die Gleichungen

${\displaystyle {\begin{matrix}\|x-{\bar {x}}\|^{2}&=&d^{2}\\f({\bar {x}})&=&0\end{matrix}}}$

beschrieben.

Die Enveloppe hat in jedem Punkt ${\displaystyle x\in A}$ mit einer der Sphären (parametrisiert durch ${\displaystyle {\bar {x}}}$) den Tangentialraum im Punkt ${\displaystyle x}$ gemeinsam. Die Tangentialvektoren ${\displaystyle dx\in \mathbb {R} ^{n}}$ an die Sphäre ${\displaystyle S_{d}({\bar {x}})}$ im Punkt ${\displaystyle x}$ genügen den Gleichungen

${\displaystyle {\begin{matrix}(1)&&f({\bar {x}})&=&0,\\(2)&&\|x-{\bar {x}}\|^{2}&=&d^{2},\\(3)&\quad &(x-{\bar {x}})^{T}dx&=&0.\end{matrix}}}$

Bei der Enveloppe ändert sich im Allgemeinen auch der Scharparameter ${\displaystyle {\bar {x}}}$. Damit ergeben sich für die Tangentialvektoren der Enveloppe außer den Gleichungen (1) und (2) mit ${\displaystyle d{\bar {x}}\in \mathbb {R} ^{n}}$ noch die Gleichungen

${\displaystyle {\begin{matrix}(4)&\quad &(x-{\bar {x}})^{T}(dx-d{\bar {x}})&=&0,\\(5)&&f'({\bar {x}})\;d{\bar {x}}&=&0.\end{matrix}}}$

Aus (3) und (4) folgt

${\displaystyle (6)\quad (x-{\bar {x}})^{T}d{\bar {x}}=0}$

für alle ${\displaystyle d{\bar {x}}}$ die zu Tangentialvektoren ${\displaystyle dx}$ im Tangentialraum der Enveloppe korrespondieren, wegen (5) also für alle

${\displaystyle d{\bar {x}}\in \ker f'({\bar {x}})=\left(\operatorname {image} \left(f'({\bar {x}})^{T}\right)\right)^{\perp }.}$

Nach (6) ergibt sich daraus

${\displaystyle (x-{\bar {x}})\in \left(\left(\operatorname {image} (f'({\bar {x}})^{T}\right)^{\perp }\right)^{\perp }=\operatorname {image} (f'({\bar {x}})^{T}),}$

woraus folgt, dass es ${\displaystyle \lambda \in \mathbb {R} ^{r}}$ mit

${\displaystyle (7)\quad (x-{\bar {x}})=f'({\bar {x}})^{T}\lambda }$

gibt.

Mit (1),(2) und (7) hat man ${\displaystyle n+r+1}$ skalare Gleichungen für die ${\displaystyle 2n+r}$ Unbekannten ${\displaystyle x,{\bar {x}},\lambda }$. Unter den gemachten Voraussetzungen definieren diese Gleichungen also eine ${\displaystyle n-1}$-dimensionale Mannigfaltigkeit, die dann gerade die Enveloppe der Sphärenschar -- sprich die Äquidistante Hyperfläche ist.

Alternative geometrische Interpretation: Die Vektoren ${\displaystyle \left(f'_{k}({\bar {x}})\right)^{T}}$ ${\displaystyle (k=1,\ldots ,r)}$ bilden eine maximale Menge linear unabhängiger Normalenvektoren auf der Mannigfaltigkeit ${\displaystyle f^{-1}(0)}$ im Punkt ${\displaystyle {\bar {x}}}$. Damit besagt Gleichung (7), dass der Vektor ${\displaystyle (x-{\bar {x}})}$ vom Punkt ${\displaystyle {\bar {x}}}$ zum zugehörigen Punkt ${\displaystyle x}$ auf der Äquidistanten genau senkrecht auf der Mannigfaltigkeit ${\displaystyle f^{-1}(0)}$ steht und Gleichung (2), dass der Punkt ${\displaystyle x}$ den Abstand ${\displaystyle d}$ von ${\displaystyle f^{-1}(0)}$ haben soll.

1. Anwendung im Formenbau: Für die Herstellung von Massenartikeln werden häufig Gießverfahren (Spritzgießen, Druckgießen, Kokillenguss usw.) angewendet. Die Gussform hat im Innern die negative Kontur des herzustellenden Artikels als Hohlraum. Für viele Artikel ist eine konstante Wandstärke ausschlaggebend. Daher hat die Beherrschung der Äquidistante in diesem Bereich eine große Bedeutung.
2. Die Äquidistanten-Funktion wird von den meisten CAD-Systemen angeboten. Beispielsweise heißt bei AUTOCAD der deutsche Befehl „versetzen“. Damit kann man beispielsweise sehr schnell eine Dränage mit vorgegebenen Abstand rund um ein Haus festlegen.
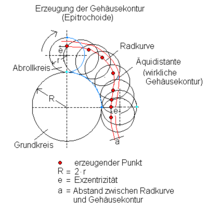
3. Beim Wankelmotor ist die Hüllkurve der Trochoide (Radkurve) des Rotors im Abstand d eine Äquidistante Hyperfläche.